
���� �٣��ձ���y���ϵĽǵļ�����{��|��=k��+$\frac{��}{2}$��k��Z����
�ڣ������εĻ���Ϊ4cm�����Ϊ4cm2�����εİ뾶rΪ��$\frac{1}{2}��4$��r=4��r=2�������ε�Բ�ĽǦ��Ļ�����Ϊ$\frac{2s}{{r}^{2}}$=2��
�ۣ�����y=cos2��$\frac{��}{4}$-x��=sin2x���溯����
�ܣ���x=$\frac{��}{6}$ʱ������y=4sin��2x-$\frac{��}{3}$��=0����$\frac{��}{6}$��0����һ���Գ����ģ�
�ݣ�����y=tan��-x-�У�=tanx��$[-�У�-\frac{��}{2}��$��������������
��� �⣺���ڢ٣��ձ���y���ϵĽǵļ�����{��|��=k��+$\frac{��}{2}$��k��Z�����ʴ���
���ڢڣ������εĻ���Ϊ4cm�����Ϊ4cm2�����εİ뾶rΪ��$\frac{1}{2}��4$��r=4��r=2�������ε�Բ�ĽǦ��Ļ�����Ϊ$\frac{2s}{{r}^{2}}$=2������ȷ��
���ڢۣ�����y=cos2��$\frac{��}{4}$-x��=sin2x���溯������ȷ��
���ڢܣ���x=$\frac{��}{6}$ʱ������y=4sin��2x-$\frac{��}{3}$��=0����$\frac{��}{6}$��0����һ���Գ����ģ�����ȷ��
���ڢݣ�����y=tan��-x-�У�=tanx��$[-�У�-\frac{��}{2}��$��������������ȷ��
�ʴ�Ϊ���ڢۢ�
���� �ۺϿ���������ٵ��ж����漰�������Ǻ�����ͼ�����ʣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ�����в���Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 2 | C�� | 1 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10m+n | B�� | 10m-n | C�� | 10mn | D�� | 10${\;}^{\frac{m}{n}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
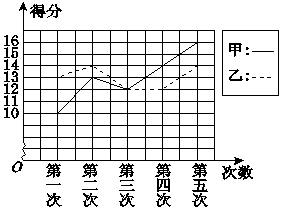 �ס��Ҷ��˲μ�ij������Ŀѵ�������ڵ���β��Գɼ��÷������ͼ��ʾ��
�ס��Ҷ��˲μ�ij������Ŀѵ�������ڵ���β��Գɼ��÷������ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12$\sqrt{2}$ | B�� | 9+$\sqrt{2}$ | C�� | 9$\sqrt{2}$ | D�� | 8+$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com