
分析 (Ⅰ)由已知利用同角三角函数基本关系式可求sinA的值,进而利用正弦定理可得sinC的值.
(Ⅱ)由sinC=$\frac{1}{3}$,c<a,利用同角三角函数基本关系式可求cosC,利用两角和的正弦函数公式可求sinB的值,进而利用三角形面积公式即可计算得解.
解答 (本题满分为13分)
解:(Ⅰ)∵cosA=$\frac{\sqrt{3}}{3}$,c=$\sqrt{3}$,a=3$\sqrt{2}$.
∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{6}}{3}$,
∴由正弦定理可得:sinC=$\frac{csinA}{a}$=$\frac{\sqrt{3}×\frac{\sqrt{6}}{3}}{3\sqrt{2}}$=$\frac{1}{3}$.
(Ⅱ)∵sinC=$\frac{1}{3}$,c<a,C为锐角,
∴cosC=$\sqrt{1-si{n}^{2}C}$=$\frac{2\sqrt{2}}{3}$,
∴sinB=sin(A+C)=sinAcosC+cosAsinC=$\frac{\sqrt{6}}{3}×\frac{2\sqrt{2}}{3}$+$\frac{\sqrt{3}}{3}×\frac{1}{3}$=$\frac{5\sqrt{3}}{9}$,
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}×3\sqrt{2}×\sqrt{3}×$$\frac{5\sqrt{3}}{9}$=$\frac{5\sqrt{2}}{2}$.
点评 本题主要考查了同角三角函数基本关系式,正弦定理,两角和的正弦函数公式,三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷(解析版) 题型:解答题
(1)用辗转相除法求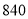 与
与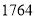 的最大公约数.
的最大公约数.
(2)用更相减损术求 与
与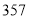 的最大公约数.
的最大公约数.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷(解析版) 题型:选择题
已知不等式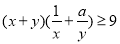 对任意正实数
对任意正实数 恒成立,则正实数
恒成立,则正实数 的最小值为( )
的最小值为( )
A. B.
B. C.
C. D.
D.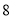
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河南省商丘市高一文下学期期末考数学试卷(解析版) 题型:解答题
已知△ABC的角A、B、C所对的边分别是a、b、c,设向量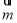 =(a,b),
=(a,b),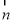 =(sin B,sin A),
=(sin B,sin A),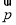 =(b-2,a-2).
=(b-2,a-2).
(Ⅰ)若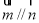 ,判断△ABC的形状;
,判断△ABC的形状;
(Ⅱ)若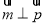 ,边长c=2,角C=
,边长c=2,角C=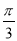 ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:解答题
已知y=f(x)是定义在R上的奇函数,且x<0时,f(x)=1+2x.
(1)求函数f(x)的解析式.
(2)画出函数f(x)的图象.
(3)写出函数f(x)单调区间及值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com