
分析 (1)运用象限角的三角函数符号化简三角函数式,求得正切值;
(2)巧用三角函数的平方关系,将整式看作分母为1的三角函数式,化为正切的式子求值.
解答 解:(1)因为θ为第二象限的角,
所以sinθ-2|cosθ|=sinθ+2cosθ=0
得tanθ=-2,
(2)sin2θ-sinθ•cosθ-2cos2θ+1
=2sin2θ-sinθ•cosθ-cos2θ
=$\frac{{2{{sin}^2}θ-sinθ•cosθ-{{cos}^2}θ}}{{{{sin}^2}θ+{{cos}^2}θ}}$
=$\frac{{2{{tan}^2}θ-tanθ-1}}{{{{tan}^2}θ+1}}$
=$\frac{{2×{{(-2)}^2}-(-2)-1}}{{{{(-2)}^2}+1}}=\frac{9}{5}$.
点评 本题考查了化简三角函数求值以及三角函数的基本关系式的应用求值;属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | (-∞,0) | C. | (-∞,1] | D. | (-∞,0)∪(0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{18}$ | B. | $-\frac{25}{18}$ | C. | $\frac{7}{18}$ | D. | $-\frac{7}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河南省商丘市高一文下学期期末考数学试卷(解析版) 题型:选择题
函数f(x)=sin xcos x+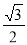 cos 2x的最小正周期和振幅分别是( )
cos 2x的最小正周期和振幅分别是( )
A.π,1 B.π,2 C.2π,1 D.2π,2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com