练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．M是z轴上一点，且到点A（1，0，2）与点B（1，-3，1）的距离相等，则点M关于原点对称的点的坐标为（0，0，3）．

    分析 设M（0，0，x），由M到点A（1，0，2）与点B（1，-3，1）的距离相等，求出M（0，0，-3），由此能求出点M关于原点对称的点的坐标．

    解答 解：∵M是z轴上一点，∴设M（0，0，x），
    ∵M到点A（1，0，2）与点B（1，-3，1）的距离相等，
    ∴$\sqrt{1+（2-x）^{2}}=\sqrt{（1+9+（1-x）^{2}}$，
    解得x=-3，∴M（0，0，-3），
    ∴点M关于原点对称的点的坐标为（0，0，3）．
    故答案为：（0，0，3）．

    点评 本题考查点的坐标的求法，是基础题，解题时要认真审题，注意两点间距离公式、对称性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．设$f（x）=\left\{\begin{array}{l}3{e^{x-1}}，x＜2\\{log_7}（8x+1），x≥2\end{array}\right.$，则f[f（ln2+1）]=（　　）
    A．2B．7C．log713D．log717

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

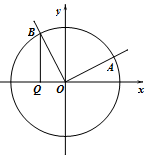    17．如图，在平面直角坐标系xOy中，角α（0≤α≤π）的始边为x轴的非负半轴，终边与单位圆的交点为A，将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB，过点B作x轴的垂线，垂足为Q．记线段BQ的长为y，则函数y=f（α）的图象大致是（　　）
    A．B．C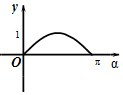．D．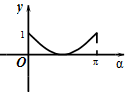

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．cos585°的值为（　　）
    A．$\frac{{\sqrt{3}}}{2}$B．$-\frac{{\sqrt{3}}}{2}$C．$\frac{{\sqrt{2}}}{2}$D．$-\frac{{\sqrt{2}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知sinθ-2|cosθ|=0，且θ为第二象限的角．
    （1）求tanθ的值；
    （2）求sin2θ-sinθ•cosθ-2cos2θ+1的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．过点（0，3）且与直线2x+y-5=0垂直的直线方程为（　　）
    A．2x+y-3=0B．x+2y-6=0C．x-2y+6=0D．2x-y+3=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．下列函数中为奇函数的是（　　）
    A．y=sin2xB．y=xcosxC．y=$\sqrt{x}$D．y=|x|

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷（解析版） 题型：解答题

    （1）用辗转相除法求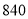与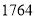的最大公约数．

    （2）用更相减损术求与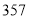的最大公约数．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年河南省商丘市高一理下学期期末考数学试卷（解析版） 题型：解答题

    如图，游客从某旅游景区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C．现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50 m/min．在甲出发2 min 后，乙从A乘缆车到B，在B处停留1 min后，再从B匀速步行到C．假设缆车匀速直线运行的速度为130 m/min，山路AC长为1 260 m，经测量，cos A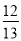＝，cos C＝．

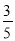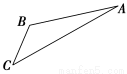
    （Ⅰ）求索道AB的长；

    （Ⅱ）问：乙出发多少分钟后，乙在缆车上与甲的距离最短？

    （Ⅲ）为使两位游客在C处互相等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？

    查看答案和解析>>

    同步练习册答案