
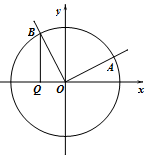
 如图,在平面直角坐标系xOy中,角α(0≤α≤π)的始边为x轴的非负半轴,终边与单位圆的交点为A,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB,过点B作x轴的垂线,垂足为Q.记线段BQ的长为y,则函数y=f(α)的图象大致是( )
如图,在平面直角坐标系xOy中,角α(0≤α≤π)的始边为x轴的非负半轴,终边与单位圆的交点为A,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB,过点B作x轴的垂线,垂足为Q.记线段BQ的长为y,则函数y=f(α)的图象大致是( )| A. |  | B. |  | C. | 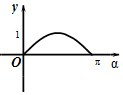 | D. | 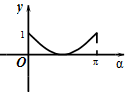 |
分析 以x轴的非负半轴为始边,OA为终边的角设为α,α∈[0,π],可得B(cos($α+\frac{π}{2}$),sin($α+\frac{π}{2}$)),即B(-sinα,cosα).记线段BQ的长为y,则函数y=f(α)=|cosα|,
解答 解:以x轴的非负半轴为始边,OA为终边的角设为α,α∈[0,π]
可得A(cosα,sinα),将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB.可得B(cos($α+\frac{π}{2}$),sin($α+\frac{π}{2}$)),
即B(-sinα,cosα).记线段BQ的长为y,则函数y=f(α)=|cosα|,
故选B.
点评 本题考查了三角函数定义的应用,考查转化思想以及计算能力,属于基础题.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | (-∞,0) | C. | (-∞,1] | D. | (-∞,0)∪(0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷(解析版) 题型:选择题
甲校有3600名学生,乙校有5400名学生,丙校有1800名学生,为统计三校学生某方面的情况,计划采用分层抽样法,抽取一个样本容量为90人的样本,则应在这三校分别抽取学生( )
A.20人,30人,10人
B.30人,30人,30人
C.30人,45人,15人
D.30人,50人,10人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com