
| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
分析 要向量组可作为这个平行四边形所在平面表示它的所有向量的基底,这两个向量必不共线(平行),画出图形,利用图象分析向量之间是否共线后,可得答案.
解答 解:如下图所示: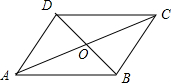
①$\overrightarrow{AD}$与$\overrightarrow{AB}$不共线,故①可作为这个平行四边形所在平面表示它的所有向量的基底;
②$\overrightarrow{DA}$与$\overrightarrow{BC}$共线,故②不可作为这个平行四边形所在平面表示它的所有向量的基底;
③$\overrightarrow{CA}$与$\overrightarrow{DC}$不共线,故③可作为这个平行四边形所在平面表示它的所有向量的基底;
④$\overrightarrow{OD}$与$\overrightarrow{OB}$共线,故④不可作为这个平行四边形所在平面表示它的所有向量的基底;
故选:B.
点评 本题以命题的真假判断为载体考查了平面向量的基本定理,熟练掌握基底的定义是解答的关键.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 7 | C. | log713 | D. | log717 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
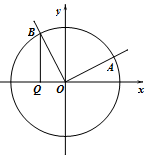 如图,在平面直角坐标系xOy中,角α(0≤α≤π)的始边为x轴的非负半轴,终边与单位圆的交点为A,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB,过点B作x轴的垂线,垂足为Q.记线段BQ的长为y,则函数y=f(α)的图象大致是( )
如图,在平面直角坐标系xOy中,角α(0≤α≤π)的始边为x轴的非负半轴,终边与单位圆的交点为A,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB,过点B作x轴的垂线,垂足为Q.记线段BQ的长为y,则函数y=f(α)的图象大致是( )| A. |  | B. |  | C. | 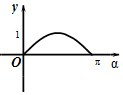 | D. | 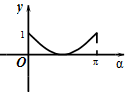 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷(解析版) 题型:解答题
(1)用辗转相除法求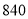 与
与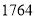 的最大公约数.
的最大公约数.
(2)用更相减损术求 与
与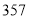 的最大公约数.
的最大公约数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com