
分析 (1)由平面向量共线的坐标表示列出方程,解方程求出x的值;
(2)根据两向量的数量积为0,即可得出它们的夹角为$\frac{π}{2}$.
解答 解:(1)向量$\overrightarrow{a}$=(1,3),$\overrightarrow{b}$=(3,x),
当$\overrightarrow{a}$∥$\overrightarrow{b}$时,1×x-3×3=0,
解得x=9; …(3分)
(2)当x=-1时,$\overrightarrow{b}$=(3,-1); …(4分)
所以$\overrightarrow{a}$•$\overrightarrow{b}$=1×3+3×(-1)=0,
所以cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=0,…(6分)
因为<$\overrightarrow{a}$,$\overrightarrow{b}$>∈[0,π],…(7分)
所以 $\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{2}$.…(8分)
点评 本题考查了平面向量的共线定理与夹角大小的计算问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{2}{13}$$\sqrt{13}$ | C. | $\frac{5}{26}$$\sqrt{13}$ | D. | $\frac{7}{20}$$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
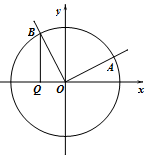 如图,在平面直角坐标系xOy中,角α(0≤α≤π)的始边为x轴的非负半轴,终边与单位圆的交点为A,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB,过点B作x轴的垂线,垂足为Q.记线段BQ的长为y,则函数y=f(α)的图象大致是( )
如图,在平面直角坐标系xOy中,角α(0≤α≤π)的始边为x轴的非负半轴,终边与单位圆的交点为A,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB,过点B作x轴的垂线,垂足为Q.记线段BQ的长为y,则函数y=f(α)的图象大致是( )| A. |  | B. |  | C. | 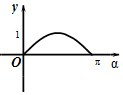 | D. | 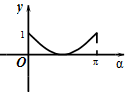 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-3=0 | B. | x+2y-6=0 | C. | x-2y+6=0 | D. | 2x-y+3=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com