
分析 (1)由所求圆与y轴相切,得到圆心的横坐标的绝对值为圆的半径,进而由圆心C的坐标和求出的半径写出圆的标准方程即可.
(2)化圆的方程为标准方程,计算圆心到直线的距离与半径比较,即可得到结论.
解答 解:(1)∵圆心O的坐标为(-4,2),且所求圆与y轴相切,
∴圆的半径r=4,
则所求圆的方程为(x+4)2+(y-2)2=16,即x2+y2+8x-4y+4=0.
(2)圆x2+y2-2x+3y=4化为标准方程为(x-1)2+(y+$\frac{3}{2}$)2=$\frac{29}{4}$,圆心坐标为(1,-$\frac{3}{2}$),半径为$\frac{\sqrt{29}}{2}$
∴圆心到直线的距离为$\frac{|2+\frac{9}{2}+5|}{\sqrt{4+9}}$=$\frac{23}{2\sqrt{13}}$<$\frac{\sqrt{29}}{2}$
∴直线与圆相交.
点评 本题考查圆的标准方程,考查直线与圆的位置关系,根据题意得到圆心横坐标的绝对值为圆的半径是解本题的关键.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
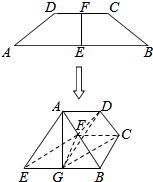 在等腰梯形ABCD中,E,F分别是AB,CD的中点,AB=4,CD=2,AD=BC=$\sqrt{2}$,现将梯形AEFD沿EF折起,并记平面AEFD与平面BEFC所成二面角的平面角为θ,BE中点为G.
在等腰梯形ABCD中,E,F分别是AB,CD的中点,AB=4,CD=2,AD=BC=$\sqrt{2}$,现将梯形AEFD沿EF折起,并记平面AEFD与平面BEFC所成二面角的平面角为θ,BE中点为G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com