
【题目】如图,正方形![]() 所在平面与等腰梯形
所在平面与等腰梯形![]() 所在平面互相垂直,已知
所在平面互相垂直,已知![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)分别证明BD垂直DE和AD,结合直线与平面垂直判定,即可.(2)建立坐标系,分别计算两个平面的法向量,结合向量数量积公式,即可.
证明:(1)因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
由余弦定理可得![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)因为四边形![]() 是等腰梯形,
是等腰梯形,![]() ,
,
又由(1)知![]() ,所以
,所以![]() ,所以
,所以![]() .
.
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线作为
所在直线作为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的坐标系,
轴建立如图所示的坐标系,
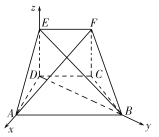
设![]() ,则
,则![]() ,可得
,可得![]() ,
,![]() ,
,
由![]() ,
,![]() ,可得,
,可得,![]() ,
,
由此可得![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则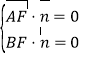 ,
,
可得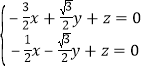 ,
,
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,
由(1)知,![]() ,
,![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
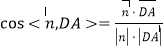
![]() .
.
所以所求锐二面角的余弦值为![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】为了迎接旅游旺季的到来,辽阳汤河风景区内供游客住宿的某宾馆,工作人员发现为游客准备的食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月入住的游客人数,现每年各个月份来宾馆入住的游客人数会呈现周期性的变化,并且有以下规律:
①每年相同的月份,入住宾馆的游客人数基本相同;
②入住宾馆的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份入住宾馆的游客约为100人,随后逐月增加直到8月份达到最多.
(1)若一年中入住宾馆的游客人数与月份之间的关系为![]() ,
,![]() 且
且![]() .试求出函数
.试求出函数![]() 的解析式;
的解析式;
(2)请问哪几个月份要准备不少于400份的食物?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)求证:对![]() 直线
直线![]() 与圆
与圆![]() 总有两个不同的交点;
总有两个不同的交点;
(2)是否存在实数![]() ,使得圆
,使得圆![]() 上有四个点到直线
上有四个点到直线![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中,![]() 是棱
是棱![]() 的中点,
的中点,![]() 是侧面
是侧面![]() 内的动点,且
内的动点,且![]() 与平面
与平面![]() 的垂线垂直,如图所示,下列说法不正确的序号为__________
的垂线垂直,如图所示,下列说法不正确的序号为__________

①点![]() 的轨迹是一条线段.②
的轨迹是一条线段.②![]() 与
与![]() 是异面直线.
是异面直线.
③![]() 与
与![]() 不可能平行.④三棱锥
不可能平行.④三棱锥![]() 的体积为定值.
的体积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周脾算经》有记载:一年有二十四个节气,每个节气晷(gui)长损益相同,晷是按照日影测定时刻的仪器,晷长即所测定的影子的长度,二十四节气及晷长变化如图所示,相邻两个节气晷长变化量相同,周而复始,若冬至晷长最长是一丈三尺五寸,夏至晷长最短是一尺五寸,(一丈等于10尺,一尺等于10寸),则秋分节气的晷长是( )
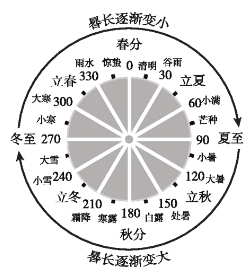
A.七尺五寸B.二尺五寸C.五尺五寸D.四尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为大力提倡“厉行节约,反对浪费”,某市通过随机调查100名性别不同的居民是否做到“光盘”行动,得到如下列联表:
| 做不到“光盘”行动 | 做到“光盘”行动 |
男 | 45 | 10 |
女 | 30 | 15 |
经计算 . 附表:
. 附表:
|
|
|
|
|
|
|
|
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过![]() 的前提下,认为“该市居民能否做到
的前提下,认为“该市居民能否做到![]() 光盘
光盘![]() 行动与性别有关”
行动与性别有关”
![]() 的前提下,认为“该市居民能否做到
的前提下,认为“该市居民能否做到![]() 光盘
光盘![]() 行动与性别无关”
行动与性别无关”
C.有![]() 以上的把握认为“该市居民能否做到
以上的把握认为“该市居民能否做到![]() 光盘
光盘![]() 行动与性别有关”
行动与性别有关”
D.有![]() 以上的把握认为“该市居民能否做到
以上的把握认为“该市居民能否做到![]() 光盘
光盘![]() 行动与性别无关”
行动与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com