
| A. | $\frac{{\sqrt{3}π}}{12}$ | B. | $\frac{{\sqrt{3}π}}{6}$ | C. | $1-\frac{{\sqrt{3}π}}{6}$ | D. | $1-\frac{{\sqrt{3}π}}{12}$ |
分析 本题考查的知识点是几何概型的意义,关键是要找出蚂蚁距离三角形的三个顶点的距离不超过1区域面积,利用面积比求概率.
解答 解:由已知得到三角形为直角三角形,三角形ABC的面积为$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,
离三个顶点距离都不大于1的地方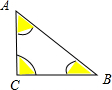 如图三角形的阴影部分,
如图三角形的阴影部分,
它的面积为半径为1的半圆面积S=$\frac{1}{2}$π×12=$\frac{π}{2}$,
所以其恰在离三个顶点距离不超过1的概率为:P=$\frac{\frac{π}{2}}{2\sqrt{3}}$=$\frac{\sqrt{3}π}{12}$.
故选:A.
点评 本题考查几何概型概率公式、三角形的面积公式、扇形的面积公式;关键是找出事件的测度是符合条件的面积.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 111 110 | B. | 1 111 111 | C. | 1 111 112 | D. | 1 111 113 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{3}}$)∪(${\frac{1}{3}$,+∞) | B. | (-∞,-$\frac{1}{3}}$]∪[${\frac{1}{3}$,+∞) | C. | (-2,-$\frac{1}{3}}$]∪[${\frac{1}{3},2}$) | D. | [-2,-$\frac{1}{3}}$]∪[${\frac{1}{3}$,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com