练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知定义在R上的偶函数f（x）满足f（x+4）=f（x），且当0≤x≤2时，f（x）=min{-x2+2x，2-x}，若方程f（x）-mx=0恰有两个实数根，则实数m的取值范围是（　　）
    A．（-∞，-$\frac{1}{3}}$）∪（${\frac{1}{3}$，+∞）B．（-∞，-$\frac{1}{3}}$]∪[${\frac{1}{3}$，+∞）C．（-2，-$\frac{1}{3}}$]∪[${\frac{1}{3}，2}$）D．[-2，-$\frac{1}{3}}$]∪[${\frac{1}{3}$，2]

    分析 首先由题意求出f（x），然后令g（x）=mx，转化为图象交点的问题解决．

    解答 解：由题意得f（x）=$\left\{\begin{array}{l}{{-x}^{2}+2x，0≤x≤1}\\{2-x，1＜x≤2}\end{array}\right.$，
    又因为f（x）是偶函数且周期是4，可得整个函数的图象，
    令g（x）=mx，本题转化为两个交点的问题，
    由图象可知有2部分组成，
    ，
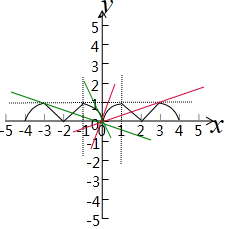    结合图象，-2＜m≤-$\frac{1}{3}$或$\frac{1}{3}$≤m＜2，
    故选：C．

    点评 本题考查的是函数的性质的综合应用，利用数形结合快速得解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．一只蚂蚁在边长分别为2，$2\sqrt{3}$，4的三角形内爬行，某时刻此此蚂蚁距离顶点三角形的距离均不超过1的概率为（　　）
    A．$\frac{{\sqrt{3}π}}{12}$B．$\frac{{\sqrt{3}π}}{6}$C．$1-\frac{{\sqrt{3}π}}{6}$D．$1-\frac{{\sqrt{3}π}}{12}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．如果函数f（x）=sin（ωx+$\frac{π}{3}$）（ω＞0）的最小正周期是π，那么f（π）=（　　）
    A．$\frac{1}{2}$B．-$\frac{1}{2}$C．$\frac{\sqrt{3}}{2}$D．-$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．（1）有20个零件，其中16个一等品，4个二等品，若从这20个零件中任意取3个，那么至少有1个一等品的不同取法有多少种？（用两种不同的方法求解）
    （2）用1、2、3、4这4个数字组成无重复数字的四位数，其中恰有1个偶数字夹在两个奇数字之间的四位数的个数有多少个？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．△ABC的内角A，B，C的对边分别为a，b，c，已知2cosC（acosB+bcosA）=c．
    （Ⅰ）求C；
    （Ⅱ）若△ABC的周长为5+$\sqrt{7}$，面积为$\frac{3\sqrt{3}}{2}$，求c．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若x，y满足约束条件$\left\{\begin{array}{l}x-1≥0\\ x-y≤0\\ x+y-4≤0\end{array}\right.$，则log3$\frac{y}{x}$的取值范围为[0，1]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知n∈N*，k∈N*，k≤n．求证：
    （1）（k+1）C${\;}_{n+1}^{k+1}$=（n+1）C${\;}_{n}^{k}$；
    （2）C${\;}_{n}^{0}$+$\frac{1}{2}$C${\;}_{n}^{1}$+$\frac{1}{3}$C${\;}_{n}^{2}$+…+$\frac{1}{n+1}$C${\;}_{n}^{n}$=$\frac{{2}^{n+1}-1}{n+1}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．求直线l1：$\left\{\begin{array}{l}{x=1+3t}\\{y=2-4t}\end{array}\right.$（t为参数）与直线l2：2x-4y=5的交点B的坐标，及点B与A（1，2）的距离．．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知双曲线的一条渐近线为y=2x，且经过抛物线y2=4x的焦点，则双曲线的标准方程为${x^2}-\frac{y^2}{4}=1$．

    查看答案和解析>>

    同步练习册答案