
分析 (1)法1:至少有1个是一等品的不同取法包括恰有1个一等品的不同取法,共有C161C42;恰有2个一等品的不同取法,共有C162C41;恰有3个一等品的不同取法,根据分类加法原理得到结果;
法2:考虑其对立事件“3个都是二等品”,用间接法可得结论;
(2)该问题可看作是一个排列问题,首先由1,3两个数字全排列,形成3个空,则2,4要么在最前边的空和1,3之间形成的空两个空中排列,要么在最后边的空和1,3之间形成的空两个空中排列,则答案可求.
解答 解:(1)法1:由题意知本题是一个分类计数问题,
至少有1个是一等品的不同取法
分三类:恰有1个一等品的不同取法,共有C161C42
恰有2个一等品的不同取法,共有C162C41
恰有3个一等品的不同取法,共有C163
由分类计数原理有:C161C42+C162C41+C163=1136种.
法2:考虑其对立事件“3个都是二等品”,用间接法,得至少有1个一等品的不同取法有C203-C163=1136种:;
(2)首先把1,3全排列,得到排法种数为A22,
则1,3之间形成三个空,2,4要么在前两个空中全排列,要么在后两个空中全排列,
∴四位数的个数为2A22A22=8.
点评 本题考查分类、分步计数原理,解题时一定要分清做这件事需要分为几类,每一类包含几种方法,把几个步骤中数字相加得到结果.本题是一个中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
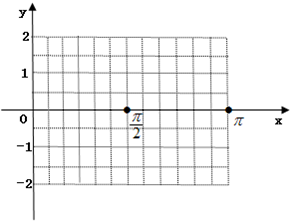 已知函数f(x)=2cos2x+2$\sqrt{3}$sinxcosx-1.
已知函数f(x)=2cos2x+2$\sqrt{3}$sinxcosx-1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$+$\frac{3}{5}$i | B. | -$\frac{1}{5}$-$\frac{3}{5}$i | C. | -$\frac{1}{5}$+$\frac{3}{5}$i | D. | $\frac{1}{5}$-$\frac{3}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{3}}$)∪(${\frac{1}{3}$,+∞) | B. | (-∞,-$\frac{1}{3}}$]∪[${\frac{1}{3}$,+∞) | C. | (-2,-$\frac{1}{3}}$]∪[${\frac{1}{3},2}$) | D. | [-2,-$\frac{1}{3}}$]∪[${\frac{1}{3}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{e}$1=(0,0),$\overrightarrow{e}$2=(1,-2) | B. | $\overrightarrow{e}$1=(-1,2),$\overrightarrow{e}$2=(5,7) | ||
| C. | $\overrightarrow{e}$1=(3,5),$\overrightarrow{e}$2=(6,10) | D. | $\overrightarrow{e}$1=(2,-3),$\overrightarrow{e}$2=($\frac{1}{2}$,-$\frac{3}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com