
分析 (1)由n∈N*,k∈N*,k≤n.利用组合数的计算公式可得(k+1)C${\;}_{n+1}^{k+1}$=(k+1)×$\frac{(n+1)!}{(k+1)!(n-k)!}$=$\frac{(n+1)•n!}{k!(n-k)!}$,即可证明.
(2)由(1)可知:$\frac{1}{k+1}{C}_{n}^{k}$=$\frac{1}{n+1}$${∁}_{n+1}^{k+1}$,再利用二项式定理的性质即可得出.
解答 证明:(1)∵n∈N*,k∈N*,k≤n.
(k+1)C${\;}_{n+1}^{k+1}$=(k+1)×$\frac{(n+1)!}{(k+1)!(n-k)!}$=$\frac{(n+1)•n!}{k!(n-k)!}$=(n+1)C${\;}_{n}^{k}$.
(2)C${\;}_{n}^{0}$+$\frac{1}{2}$C${\;}_{n}^{1}$+$\frac{1}{3}$C${\;}_{n}^{2}$+…+$\frac{1}{n+1}$C${\;}_{n}^{n}$=$\frac{{2}^{n+1}-1}{n+1}$.
(2)由(1)可知:$\frac{1}{k+1}{C}_{n}^{k}$=$\frac{1}{n+1}$${∁}_{n+1}^{k+1}$,
令k=0,1,2,3,…,n,得:C${\;}_{n}^{0}$+$\frac{1}{2}$C${\;}_{n}^{1}$+$\frac{1}{3}$C${\;}_{n}^{2}$+…+$\frac{1}{n+1}$C${\;}_{n}^{n}$=$\frac{1}{n+1}$(${∁}_{n+1}^{1}$+${∁}_{n+1}^{2}$+…+${∁}_{n+1}^{n+1}$)=$\frac{1}{n+1}$[(1+1)n+1-1]=
$\frac{{2}^{n+1}-1}{n+1}$.
∴原式得证.
点评 本题考查了二项式定理的应用、组合数的性质,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 111 110 | B. | 1 111 111 | C. | 1 111 112 | D. | 1 111 113 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{3}}$)∪(${\frac{1}{3}$,+∞) | B. | (-∞,-$\frac{1}{3}}$]∪[${\frac{1}{3}$,+∞) | C. | (-2,-$\frac{1}{3}}$]∪[${\frac{1}{3},2}$) | D. | [-2,-$\frac{1}{3}}$]∪[${\frac{1}{3}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
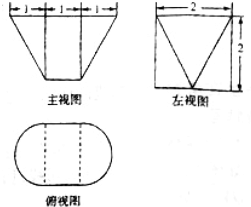 如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )
如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )| A. | 6+$\frac{2π}{3}$ | B. | 8+$\frac{π}{3}$ | C. | 4+$\frac{2π}{3}$ | D. | 4+$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S=1+2+3+…+10000000 | B. | S=1+2+3+4 | ||
| C. | S=1+2+3+…+n(n≥2且n∈N) | D. | S=12+22+32+…+1002 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com