
【题目】在△ABC中,已知AB= ![]() ,cosB=
,cosB= ![]() ,AC边上的中线BD=
,AC边上的中线BD= ![]() ,求sinA的值.
,求sinA的值.
【答案】解:解法一:设E为BC的中点,连接DE,则DE∥AB,且DE= ![]() AB=
AB= ![]() ,设BE=x.
,设BE=x.
由DE∥AB可得出∠BED=π﹣∠B,即cos∠BED=﹣ ![]()
在△BDE中利用余弦定理可得:BD2=BE2+ED2﹣2BEEDcos∠BED,5=x2+ ![]() +2×
+2× ![]() ×
× ![]() x,
x,
解得x=1,x=﹣ ![]() (舍去).
(舍去).
故BC=2,从而AC2=AB2+BC2﹣2ABBCcosB= ![]() ,即AC=
,即AC= ![]()
又sinB= ![]() ,故
,故 ![]() =
= ![]() ,sinA=
,sinA= ![]() .
.
解法二:以B为坐标原点, ![]() 为x轴正向建立直角坐标系,且不妨设点A位于第一象限.
为x轴正向建立直角坐标系,且不妨设点A位于第一象限.
由sinB= ![]() ,则
,则 ![]() =(
=( ![]() cosB,
cosB, ![]() sinB)=(
sinB)=( ![]() ,
, ![]() ),
),
设 ![]() =(x,0),则
=(x,0),则 ![]() =(
=( ![]() ,
, ![]() ).
).
由条件得| ![]() |=
|=  =
= ![]() .
.
从而x=2,x=﹣ ![]() (舍去).故
(舍去).故 ![]() =(﹣
=(﹣ ![]() ,
, ![]() ).
).
于是cosA= 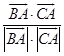 =
= 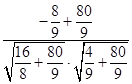 =
= ![]() .
.
∴sinA= ![]() =
= ![]() .
.
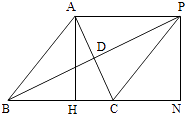
解法三:过A作AH⊥BC交BC于H,延长BD到P使BD=DP,连接AP、PC.
过P做PN⊥BC交BC的延长线于N,则HB=ABcosB= ![]() ,AH=
,AH= ![]() ,
,
BN= ![]() =
= ![]() =
= 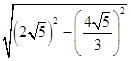 =
= ![]() ,
,
而 HB= ![]() ,∴CN=
,∴CN= ![]() ,HC=
,HC= ![]() ,AC=
,AC= ![]() =
= ![]() .
.
故由正弦定理得 ![]() =
= ![]() ,∴sinA=
,∴sinA= ![]() .
.
【解析】解三角形的特征是把题目中所给的条件全部集合到一个三角形中,依次解出边、角,达到解三角形的目的.
方法一通过充分利用D是中点,构造新三角形,在新三角形中解出BC的一半求出BC,再由余弦定理求边AC,下则可用正弦定理求出sinA;
方法二根据所给的条件巧妙地建立了一个直角坐标系,将三角问题转化到向量中研究,大大降低了分析问题的难度,首先是求出了 ![]() ,
, ![]() 两个向量,利用公式求出了两个向量的夹角A的余弦,再求正弦.此法越过了构造新三角形,使得方法易想.
两个向量,利用公式求出了两个向量的夹角A的余弦,再求正弦.此法越过了构造新三角形,使得方法易想.
方法三与方法一类似构造了一系列的新三角形,此方法充分利用D是中点这一性质构造出了一个平行四边形,使得求三角形的另两边的边长时视野开阔,方法也较巧妙.
【考点精析】根据题目的已知条件,利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示.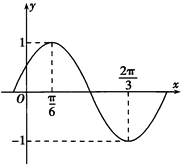
(1)求函数f(x)的解析式,并写出f(x)的单调减区间;
(2)已知△ABC的内角分别是A,B,C,A为锐角,且f ![]() ,求cosA的值.
,求cosA的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为正项数列{an}的前n项和,a1=2,Sn+1(Sn+1﹣2Sn+1)=3Sn(Sn+1),则a100等于( )
A.2×398
B.4×398
C.2×399
D.4×399
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】ABCD为空间四边形,AB=CD,AD=BC,AB≠AD,M,N分别是对角线AC与BD的中点,则MN与( )
A.AC,BD之一垂直
B.AC,BD都垂直
C.AC,BD都不垂直
D.AC,BD不一定垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解学生遵守《中华人民共和国交通安全法》的情况,调查部门在某学校进行了如下的随机调查:向被调查者提出两个问题:(1)你的学号是奇数吗?(2)在过路口的时候你是否闯过红灯?要求被调查者背对调查人抛掷一枚硬币,如果出现正面,就回答第(1)个问题;否则就回答第(2)个问题.被调查者不必告诉调查人员自己回答的是哪一个问题,只需要回答“是”或“不是”,因为只有被调查本人知道回答了哪个问题,所以都如实做了回答.如果被调查的600人(学号从1到600)中有180人回答了“是”,由此可以估计在这600人中闯过红灯的人数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率为 ![]() ,短轴长为4
,短轴长为4 ![]() . (Ⅰ)求椭圆C的标准方程;
. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)直线x=2与椭圆C交于P、Q两点,A、B是椭圆O上位于直线PQ两侧的动点,且直线AB的斜率为 ![]() .
.
①求四边形APBQ面积的最大值;
②设直线PA的斜率为k1 , 直线PB的斜率为k2 , 判断k1+k2的值是否为常数,并说明理由.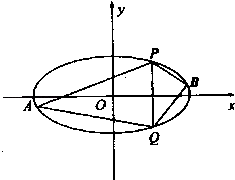
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com