
【题目】设Sn为正项数列{an}的前n项和,a1=2,Sn+1(Sn+1﹣2Sn+1)=3Sn(Sn+1),则a100等于( )
A.2×398
B.4×398
C.2×399
D.4×399
【答案】B
【解析】解:Sn为正项数列{an}的前n项和,a1=2,Sn+1(Sn+1﹣2Sn+1)=3Sn(Sn+1), 可得Sn+12﹣2Sn+1Sn﹣3Sn2+Sn+1﹣3Sn=0,
即有(Sn+1﹣3Sn)(Sn+1+Sn)+(Sn+1﹣3Sn)=0,
即为(Sn+1﹣3Sn)(Sn+1+Sn+1)=0,
即有Sn+1=3Sn ,
数列{Sn}为等比数列,首项为2,公比为3,
可得Sn=2×3n﹣1 ,
则a100=S100﹣S99=2×399﹣2×398
=4×398 .
故选:B.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系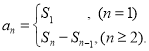 才能正确解答此题.
才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
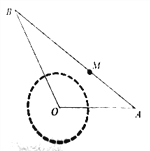
【题目】某综艺频道举行某个水上娱乐游戏,如图,固定在水面上点![]() 处的某种设备产生水波圈,水波圈生产
处的某种设备产生水波圈,水波圈生产![]() 秒时的半径
秒时的半径![]() (单位:
(单位: ![]() )满足
)满足![]() ;
; ![]() 是铺设在水面上的浮桥,浮桥的宽度忽略不计,浮桥两端
是铺设在水面上的浮桥,浮桥的宽度忽略不计,浮桥两端![]() 固定在水岸边.游戏规定:当点
固定在水岸边.游戏规定:当点![]() 处刚产生水波圈时,游戏参与者(视为一个点)与此同时从浮桥的
处刚产生水波圈时,游戏参与者(视为一个点)与此同时从浮桥的![]() 端跑向
端跑向![]() 端;若该参与者通过浮桥
端;若该参与者通过浮桥![]() 的过程中,从点
的过程中,从点![]() 处发出的水波圈始终没能到达此人跑动时的位置,则认定该参与者在这个游戏中过关;否则认定在这个游戏中不过关,已知
处发出的水波圈始终没能到达此人跑动时的位置,则认定该参与者在这个游戏中过关;否则认定在这个游戏中不过关,已知![]() ,
, ![]() ,浮桥
,浮桥![]() 的某个桥墩处点
的某个桥墩处点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,且
,且![]() ,若某游戏参与者能以
,若某游戏参与者能以![]() 的速度从浮桥
的速度从浮桥![]() 端匀速跑到
端匀速跑到![]() 端.
端.
(1)求该游戏参与者从浮桥![]() 端跑到
端跑到![]() 端所需的时间?
端所需的时间?
(2)问该游戏参与者能否在这个游戏中过关?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的叙述,错误的个数为( )
①若p∨q为真命题,则p∧q为真命题
②“x>5”是“x2﹣4x﹣5>0”的充分不必要条件
③命题p:x∈R,使得x2+x﹣1<0,则¬p:x∈R,使得x2+x﹣1≥0
④命题“若x2﹣3x+2=0,则x=1或x=2”的逆否命题为“若x≠1或x≠2,则x2﹣3x+2≠0”
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C为△ABC的三个内角,且其对边分别为a、b、c,若cosBcosC﹣sinBsinC= ![]() .
.
(1)求角A;
(2)若a=2 ![]() ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}中,a2=4,a4+a7=15.
(1)求数列{an}的通项公式;
(2)设bn=2 ![]() +n,求b1+b2+b3+…+b10的值.
+n,求b1+b2+b3+…+b10的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,三个内角是A,B,C的对边分别是a,b,c,其中c=10,且 ![]() .
.
(1)求证:△ABC是直角三角形;
(2)设圆O过A,B,C三点,点P位于劣弧AC上,∠PAB=60°,求四边形ABCP的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com