
【题目】2018年非洲猪瘟在东北三省出现,为了进行防控,某地生物医药公司派出技术人员对当地甲乙两个养殖场提供技术服务,方案和收费标准如下:
方案一,公司每天收取养殖场技术服务费40元,对于需要用药的每头猪收取药费2元,不需要用药的不收费;
方案二,公司每天收取养殖场技术服务费120元,若需要用药的猪不超过45头,不另外收费,若需要用药的猪超过45头,超过部分每天收取药费8元.
(1)设日收费为![]() (单位:元),每天需要用药的猪的数量为
(单位:元),每天需要用药的猪的数量为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)若该医药公司从10月1日起对甲养殖场提供技术服务,10月31日该养殖场对其中一个猪舍9月份和10月份猪的发病数量进行了统计,得到如下![]() 列联表.
列联表.
9月份 | 10月份 | 合计 | |
未发病 | 40 | 85 | 125 |
发病 | 65 | 20 | 85 |
合计 | 105 | 105 | 210 |
根据以上列联表,判断是否有![]() 的把握认为猪未发病与医药公司提供技术服务有关.
的把握认为猪未发病与医药公司提供技术服务有关.
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
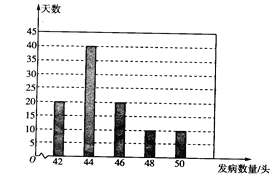
(3)当地的丙养殖场对过去100天猪的发病情况进行了统计,得到如上图所示的条形统计图.依据该统计数据,从节约养殖成本的角度去考虑,若丙养殖场计划结合以往经验从两个方案中选择一个,那么选择哪个方案更合适,并说明理由.
【答案】(1)见解析;(2)有99.9%的把握认为猪未发病与医药公司提供技术服务有关;(3)从节约养殖成本的角度去考虑,丙养殖场应该选择方案二.
【解析】
(1)根据题意写出函数关系式即可;
(2)根据![]() 列联表,代入公式计算
列联表,代入公式计算![]() ,比较临界值得出结论即可;
,比较临界值得出结论即可;
(3)分别按不同方案计算总费用,比较大小即可求解.
(1)方案一,![]() ,
,
方案二,![]()
(2)![]() ,
,
所以有99.9%的把握认为猪未发病与医药公司提供技术服务有关;
(3)若采用方案一,则这100天的总费用为
40×100+2×(42×20+44×40+46×20+48×10+50×10)=13000元,
若采用方案二,则这100天的总费用为
120×100+(46-45)×20×8+(48-45)×10×8+(50-45)×10×8=12800元,
所以,从节约养殖成本的角度去考虑,丙养殖场应该选择方案二


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图(1),在平面五边形![]() 中,已知四边形
中,已知四边形![]() 为正方形,
为正方形,![]() 为正三角形.沿着
为正三角形.沿着![]() 将四边形
将四边形![]() 折起得到四棱锥
折起得到四棱锥![]() ,使得平面
,使得平面![]() 平面
平面![]() ,设
,设![]() 在线段
在线段![]() 上且满足
上且满足![]() ,
,![]() 在线段
在线段![]() 上且满足
上且满足![]() ,
,![]() 为
为![]() 的重心,如图(2).
的重心,如图(2).
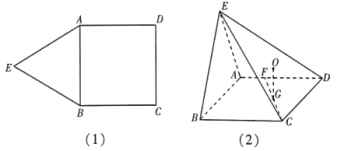
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(Ⅰ)求直线![]() 与曲线
与曲线![]() 公共点的极坐标;
公共点的极坐标;
(Ⅱ)设过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() 是正三角形,
是正三角形,![]() 与
与![]() 的交点
的交点![]() 恰好是
恰好是![]() 中点,又
中点,又![]() ,
,![]() .
.
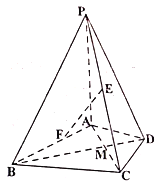
(1)求证:![]() ;
;
(2)设![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,若直线
上,若直线![]() 平面
平面![]() ,求
,求![]() 的长;
的长;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() ),其中离心率
),其中离心率![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 为椭圆的左右焦点,若
为椭圆的左右焦点,若![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 的上顶点,若
的上顶点,若![]() ,试问直线
,试问直线![]() 是否经过定点,若经过定点,求出定点坐标,否则说明理由.
是否经过定点,若经过定点,求出定点坐标,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个五位自然数![]() 数称为“跳跃数”,如果同时有
数称为“跳跃数”,如果同时有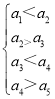 或
或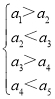 (例如13284,40329都是“跳跃数”,而12345,54371,94333都不是“跳跃数”),则由1,2,3,4,5组成没有重复数字且1,4不相邻的“跳跃数”共有_____个.
(例如13284,40329都是“跳跃数”,而12345,54371,94333都不是“跳跃数”),则由1,2,3,4,5组成没有重复数字且1,4不相邻的“跳跃数”共有_____个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是R上的偶函数,对于
是R上的偶函数,对于![]() 都有
都有![]() 成立,且
成立,且![]() ,当
,当![]() ,且
,且![]() 时,都有
时,都有![]() .则给出下列命题:
.则给出下列命题:
①![]() ;
;
②函数![]() 图象的一条对称轴为
图象的一条对称轴为![]() ;
;
③函数![]() 在[﹣9,﹣6]上为减函数;④方程
在[﹣9,﹣6]上为减函数;④方程![]() 在[﹣9,9]上有4个根;
在[﹣9,9]上有4个根;
其中正确的命题序号是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com