
【题目】已知椭圆C:![]() (
(![]() ),其中离心率
),其中离心率![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 为椭圆的左右焦点,若
为椭圆的左右焦点,若![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 的上顶点,若
的上顶点,若![]() ,试问直线
,试问直线![]() 是否经过定点,若经过定点,求出定点坐标,否则说明理由.
是否经过定点,若经过定点,求出定点坐标,否则说明理由.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某企业要设计制造一批大小、规格相同的长方体封闭水箱,已知每个水箱的表面积为432(每个水箱的进出口所占面积与制作材料的厚度均忽略不计).每个长方体水箱的底面长是宽的2倍.现设每个长方体水箱的底面宽是![]() ,用
,用![]() 表示每个长方体水箱的容积.
表示每个长方体水箱的容积.
(1)试求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)当![]() 为何值时,
为何值时,![]() 有最大值,并求出最大值.
有最大值,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a,b∈R).
(a,b∈R).
(1)若f(x)在点(1,f(1))的切线为y=x+1,求f(x)的单调性与极值;
(2)若b=﹣1,函数![]() 有且只有一个零点,求实数a的取值范围.
有且只有一个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次高三年级统一考试中,数学试卷有一道满分10分的选做题,学生可以从![]() ,
,![]() 两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名考生的选做题成绩中随机抽取一个容量为10的样本,为此将900名考生选做题的成绩按照随机顺序依次编号为001—900.
两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名考生的选做题成绩中随机抽取一个容量为10的样本,为此将900名考生选做题的成绩按照随机顺序依次编号为001—900.
(1)若采用随机数表法抽样,并按照以下随机数表,以加粗的数字5为起点,从左向右依次读取数据,每次读取三位随机数,一行读数用完之后接下一行左端.写出样本编号的中位数;
05 26 93 70 60 22 35 85 15 13 92 03 51 59 77 59 56 78 06 83 52 91 05 70 74
07 97 10 88 23 09 98 42 99 64 61 71 62 99 15 06 51 29 16 93 58 05 77 09 51
51 26 87 85 85 54 87 66 47 54 73 32 08 11 12 44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70 42 10 50 67 42 32 17 55 85 74 94 44 67 16 94
14 65 52 68 75 87 59 36 22 41 26 78 63 06 55 13 08 27 01 50 15 29 39 39 43
(2)若采用系统抽样法抽样,且样本中最小编号为08,求样本中所有编号之和:
(3)若采用分层轴样,按照学生选择![]() 题目或
题目或![]() 题目,将成绩分为两层,且样本中
题目,将成绩分为两层,且样本中![]() 题目的成绩有8个,平均数为7,方差为4:样本中
题目的成绩有8个,平均数为7,方差为4:样本中![]() 题目的成绩有2个,平均数为8,方差为1.用样本估计900名考生选做题得分的平均数与方差.
题目的成绩有2个,平均数为8,方差为1.用样本估计900名考生选做题得分的平均数与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年非洲猪瘟在东北三省出现,为了进行防控,某地生物医药公司派出技术人员对当地甲乙两个养殖场提供技术服务,方案和收费标准如下:
方案一,公司每天收取养殖场技术服务费40元,对于需要用药的每头猪收取药费2元,不需要用药的不收费;
方案二,公司每天收取养殖场技术服务费120元,若需要用药的猪不超过45头,不另外收费,若需要用药的猪超过45头,超过部分每天收取药费8元.
(1)设日收费为![]() (单位:元),每天需要用药的猪的数量为
(单位:元),每天需要用药的猪的数量为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)若该医药公司从10月1日起对甲养殖场提供技术服务,10月31日该养殖场对其中一个猪舍9月份和10月份猪的发病数量进行了统计,得到如下![]() 列联表.
列联表.
9月份 | 10月份 | 合计 | |
未发病 | 40 | 85 | 125 |
发病 | 65 | 20 | 85 |
合计 | 105 | 105 | 210 |
根据以上列联表,判断是否有![]() 的把握认为猪未发病与医药公司提供技术服务有关.
的把握认为猪未发病与医药公司提供技术服务有关.
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
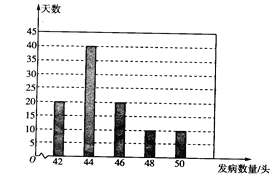
(3)当地的丙养殖场对过去100天猪的发病情况进行了统计,得到如上图所示的条形统计图.依据该统计数据,从节约养殖成本的角度去考虑,若丙养殖场计划结合以往经验从两个方案中选择一个,那么选择哪个方案更合适,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0)的离心率e
1(a>b>0)的离心率e![]() ,且点P(
,且点P(![]() ,1)在椭圆C上.
,1)在椭圆C上.
(1)求椭圆C的方程;
(2)若椭圆C的左焦点为F,右顶点为A,点M(s,t)(t>0)是椭圆C上的动点,直线AM与y轴交于点D,点E是y轴上一点,EF⊥DF,EA与椭圆C交于点G,若△AMG的面积为2![]() ,求直线AM的方程.
,求直线AM的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为:
的参数方程为: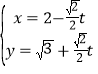 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专章规定.草案提出,国家推行生活垃圾分类制度.为了了解人民群众对垃圾分类的认识,某市环保部门对该市市民进行了一次垃圾分类网络知识问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如表所示:
得分 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,市环保部门为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() “的可以获赠2次随机话费,得分低于
“的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;②若
;②若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com