
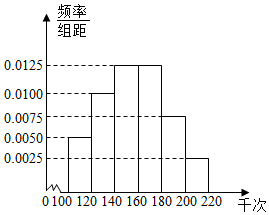
 2015年12月16日到18日第二届世界互联网大会在乌镇举行,17日奇虎360董事长周鸿祎在回答海外网记者的提问时,分享了过去100天中国每天遭受DDOS攻击的次数数据,并根据数据作出频率分布直方图,如图所示
2015年12月16日到18日第二届世界互联网大会在乌镇举行,17日奇虎360董事长周鸿祎在回答海外网记者的提问时,分享了过去100天中国每天遭受DDOS攻击的次数数据,并根据数据作出频率分布直方图,如图所示分析 (1)设A1表示事件“每天遭受DDOS攻击次数的数值高于180”,A2表示事件“每天遭受DDOS攻击次数的数值低于120”,B表示事件“在未来3天中,有连续2天的数值高于180,另一天低于120”.由此能求出在未来3天中,有连续2天的数值高于180,另一天低于120的概率.
(2)由题意,X~B(3,0.1),由此能求出X的分布列和数学期望.
解答 解:(1)设A1表示事件“每天遭受DDOS攻击次数的数值高于180”,A2表示事件“每天遭受DDOS攻击次数的数值低于120”,
B表示事件“在未来3天中,有连续2天的数值高于180,另一天低于120”.
∴P(A1)=(0.0075+0.0025)×20=0.2,
P(A2)=0.0050×20=0.1.
∴在未来3天中,有连续2天的数值高于180,另一天低于120的概率:
P(B)=0.2×0.2×0.1+0.1×0.2×0.2=0.008.
(2)由题意,X~B(3,0.2),
P(X=0)=${C}_{3}^{0}(0.8)^{3}$=0.512,
$P(X=1)={C}_{3}^{1}(0.2)(0.8)^{2}$=0.384,
P(X=2)=${C}_{3}^{2}(0.2)^{2}•0.8$=0.096,
P(X=3)=${C}_{3}^{3}(0.2)^{3}$=0.008.
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | 0.512 | 0.384 | 0.096 | 0.008 |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin(α+β)=cosαsinβ+sinαcosβ | B. | cos(α+β)=cosαcosβ+sinαsinβ | ||
| C. | sin(α-β)=cosαsinβ-sinαcosβ | D. | cos(α-β)=cosαcosβ-sinαsinβ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
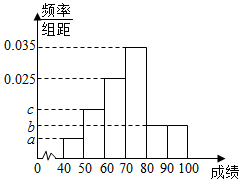 已知某班n名同学的数学测试成绩(单位:分,满分100分)的频率分布直方图如图所示,其中a,b,c成等差数列,且成绩在[90,100]内的有6人.
已知某班n名同学的数学测试成绩(单位:分,满分100分)的频率分布直方图如图所示,其中a,b,c成等差数列,且成绩在[90,100]内的有6人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
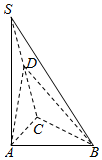 如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 42 | C. | 46 | D. | 56 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com