Question

【题目】已知各项均为正数的两个数列和{}满足：an＋1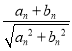＝，n∈N*.

(1)设bn＋1＝1＋，n∈N*，求证：数列是等差数列；

(2)设bn＋1＝·，n∈N*，且是等比数列，求a1和b1的值.

Answer 1

【答案】（1）见解析；（2）a1＝b1＝.

【解析】试题分析：（1）由an＋1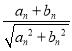＝，等式右边分子分母同时除以，再将bn＋1＝1＋带入可得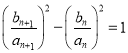，从而得证；

（2）由不等式性质有： 进而得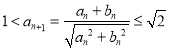，设等比数列{an}的公比为q，由反证法可得q＝1，故an＝a1(n∈N*)，所以1＜a1≤，从而得{bn}是公比为的等比数列,亦可由反证法得a1＝.

试题解析：

(1)证明　由题设知an＋1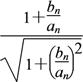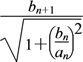＝＝＝，所以＝，

从而－＝1(n∈N*)，

所以数列是以1为公差的等差数列.

(2)解　因为an＞0，bn＞0，

所以≤a＋b＜(an＋bn)2，

从而1＜an＋1＝≤.(*)

设等比数列{an}的公比为q，由an＞0知q＞0.下证q＝1.

若q＞1，则a1＝＜a2≤，故当n＞logq时，an＋1＝a1qn＞，与(*)矛盾；

若0＜q＜1，则a1＝＞a2＞1，故当n＞logq时，an＋1＝a1qn＜1，与(*)矛盾.

综上，q＝1，故an＝a1(n∈N*)，

所以1＜a1≤.

又bn＋1＝·＝·bn(n∈N*)，所以{bn}是公比为的等比数列.

若a1≠，则＞1，于是b1＜b2＜b3.

又由a1＝得bn＝ (n∈N*)，所以b1，b2，b3中至少有两项相同，矛盾，

所以a1＝，从而bn＝＝.

所以a1＝b1＝.