
已知函数f(x)=x3+3|x-a|(a>0),若f(x)在[-1,1]上的最小值记为g(a).
(1)求g(a);
(2)证明:当x∈[-1,1]时,恒有f(x)≤g(a)+4.
①当0<a<1时,
若x∈[-1,a],则f(x)=x3-3x+3a,f′(x)=3x2-3<0,故f(x)在(-1,a)上是减函数;
若x∈[a,1],则f(x)=x3+3x-3a,f′(x)=3x2+3>0,故f(x)在(a,1)上是增函数.
所以g(a)=f(a)=a3.
②当a≥1时,有x≤a,则f(x)=x3-3x+3a,f′(x)=3x2-3<0,故f(x)在(-1,1)上是减函数,所以g(a)=f(1)=-2+3a.
综上,g(a)=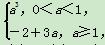
(2)证明 令h(x)=f(x)-g(a),
①当0<a<1时,g(a)=a3.
若x∈[a,1],h(x)=x3+3x-3a-a3,得h′(x)=3x2+3,则h(x)在(a,1)上是增函数,所以,h(x)在[a,1]上的最大值是h(1)=4-3a-a3,且0<a<1,所以h(1)≤4.故f(x)≤g(a)+4;
若x∈[-1,a],h(x)=x3-3x+3a-a3,得h′(x)=3x2-3,则h(x)在(-1,a)上是减函数,所以,h(x)在[-1,a]上的最大值是h(-1)=2+3a-a3.
令t(a)=2+3a-a3,则t′(a)=3-3a2>0,
知t(a)在(0,1)上是增函数.所以,t(a)<t(1)=4,即h(-1)<4.
故f(x)≤g(a)+4.
②当a≥1时,g(a)=-2+3a,故h(x)=x3-3x+2,得h′(x)=3x2-3,
此时h(x)在(-1,1)上是减函数,因此h(x)在[-1,1]上的最大值是h(-1)=4.故f(x)≤g(a)+4.
综上,当x∈[-1,1]时,恒有f(x)≤g(a)+4.


科目:高中数学 来源: 题型:
定义“等和数列”:在一个数列中,如果每一项与它后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.已知数列{an}是等和数列,且a1=-1,公和为1,那么这个数列的前2 011项和S2 011=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
设 ,椭圆方程为
,椭圆方程为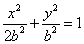 ,抛物线方程为
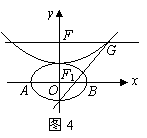
,抛物线方程为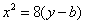 .如图4所示,过点
.如图4所示,过点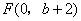 作
作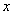 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为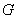 ,已知抛物线在点
,已知抛物线在点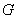 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点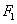 .
.
(1)求满足条件的椭圆方程和抛物线方程;
 (2)设
(2)设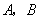 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点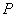 ,使得
,使得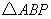 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=k(x-1)ex+x2.
(1)当k=- 时,求函数f(x)在点(1,1)处的切线方程;
时,求函数f(x)在点(1,1)处的切线方程;
(2)若在y轴的左侧,函数g(x)=x2+(k+2)x的图象恒在f(x)的导函数f′(x)图象的上方,求k的取值范围;
(3)当k≤-1时,求函数f(x)在[k,1]上的最小值m.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的通项公式an=log2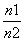 (n∈N*),设{an}的前n项和为Sn,则使Sn<-5成立的自然数 n( )
(n∈N*),设{an}的前n项和为Sn,则使Sn<-5成立的自然数 n( )
A.有最大值63 B.有最小值63
C.有最大值31 D.有最小值31
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com