
设 ,椭圆方程为
,椭圆方程为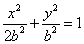 ,抛物线方程为
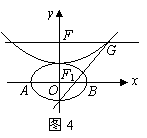
,抛物线方程为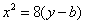 .如图4所示,过点
.如图4所示,过点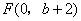 作
作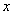 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为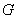 ,已知抛物线在点
,已知抛物线在点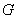 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点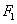 .
.
(1)求满足条件的椭圆方程和抛物线方程;
 (2)设
(2)设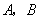 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点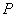 ,使得
,使得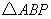 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
科目:高中数学 来源: 题型:
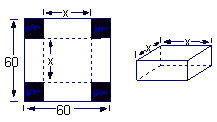
在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图) ,做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
,做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
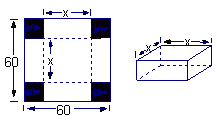 在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图)
在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图) ,做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大
,做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大 容积是多少?
容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-3x.则函数g(x)=f(x)-x+3的零点的集合为( )
A.{1,3} B.{-3,-1,1,3}
C.{2-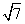 ,1,3} D.{-2-
,1,3} D.{-2-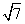 ,1,3}
,1,3}
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x3+3|x-a|(a>0),若f(x)在[-1,1]上的最小值记为g(a).
(1)求g(a);
(2)证明:当x∈[-1,1]时,恒有f(x)≤g(a)+4.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知定义在R上的函数f(x),g(x)满足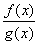 =ax,且f′(x)g(x)<f(x)g′(x),
=ax,且f′(x)g(x)<f(x)g′(x),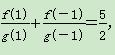 ,若有穷数列
,若有穷数列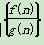 (n∈N*)的前n项和等于
(n∈N*)的前n项和等于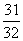 ,则n等于( )
,则n等于( )
A.4 B.5 C.6 D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com