
分析 (1)对k分类讨论,研究函数f(x)的单调性,利用单调性求出函数的最小值,将f(x)≥1恒成立等价转化为f(x)min≥1,即$\frac{2}{k}$≥1,构造函数g(x)=x-xlnx(x>0),利用导数确定出g(x)的最值,从而判定$\frac{2}{k}$=1,即可求出k的值;
(2)先证$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<f′(x2),运用分析法分析出只要证${e}^{k({x}_{1}-{x}_{2})}$-k(x1-x2)-1>0即可,通过构造函数h(x)=ex-x-1>0在(-∞,0)上恒成立,即可证得${e}^{k({x}_{1}-{x}_{2})}$-k(x1-x2)-1>0,从而证得$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<f′(x2),同理可证f′(x2)<$\frac{f({x}_{3})-f({x}_{2})}{{x}_{3}-{x}_{2}}$,即可证得结论
解答 解:(1)∵f(x)的定义域为R,f′(x)=kekx-2,
①若k<0时,f′(x)恒小于零,则f(x)在R上单调递减;
∵当x>0时,f(x)<f(0)=1,
∴不符合f(x)≥1恒成立.
②若k>0时,令f′(x)=0,得x=$\frac{1}{k}$ln$\frac{2}{k}$,
当x<$\frac{1}{k}$ln$\frac{2}{k}$时,f′(x)<0,可知f(x)在(-∞,$\frac{1}{k}$ln$\frac{2}{k}$)单调递减,
当x>$\frac{1}{k}$ln$\frac{2}{k}$时,f′(x)>0,可知f(x)在($\frac{1}{k}$ln$\frac{2}{k}$,+∞)单调递增,
∴f(x)min=f($\frac{1}{k}$ln$\frac{2}{k}$)=$\frac{2}{k}$-$\frac{2}{k}$ln$\frac{2}{k}$,
∵f(x)≥1恒成立,即f(x)min≥1,
∴$\frac{2}{k}$-$\frac{2}{k}$ln$\frac{2}{k}$≥1,
构造函数g(x)=x-xlnx(x>0),
∴g′(x)=1-lnx-1=-lnx,
∴g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴g(x)≤g(1)=1,当且仅当x=1时取得最大值1,
∴$\frac{2}{k}$=1,
∴k=2.
(2)由已知可知,f′(x2)=k${e}^{k{x}_{2}}$-2≥0,则k>0,
先证$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<f′(x2),
∵x2-x1>0,
要证$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<f′(x2),
只要证f(x2)-f(x1)<(x2-x1)(k${e}^{k{x}_{2}}$-2),即证k${e}^{k{x}_{2}}$-${e}^{k{x}_{1}}$<k(x2-x1)k${e}^{k{x}_{2}}$,
只要证1-${e}^{k({x}_{1}-{x}_{2})}$<k(x2-x1),即证${e}^{k({x}_{1}-{x}_{2})}$-k(x1-x2)-1>0,
设h(x)=ex-x-1,
∵h′(x)=ex-1<0,
∴h(x)在(-∞,0)内是减函数,
∴h(x)>h(0)=0,
∵x=k(x1-x2)<0,
∴h(k(x1-x2))>0,
∴$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<f′(x2),
同理可证f′(x2)<$\frac{f({x}_{3})-f({x}_{2})}{{x}_{3}-{x}_{2}}$.
∴$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<f′(x2)<$\frac{f({x}_{3})-f({x}_{2})}{{x}_{3}-{x}_{2}}$.
点评 本题主要考查了导数在最大值和最小值中的应用,考查了利用导数研究函数的单调性以及用导数解决方程根的分布的问题,同时考查了利用构造函数法证明不等式,是一道综合题,有一定的难度.属于难题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3] | B. | (-∞,-3) | C. | [-3,-$\frac{1}{2}$) | D. | (-3,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
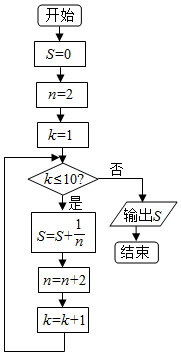
| A. | S=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{10}$ | B. | S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$ | ||
| C. | S=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{11}$ | D. | S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{22}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪{1} | B. | (-∞,1] | C. | (0,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参与调查问卷次数 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) | [10,12] |
| 参与调查问卷人数 | 8 | 14 | 8 | 14 | 10 | 6 |
| P(x2>k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3,841 | 6.635 |
| 男 | 女 | 合计 | |
| 积极上网参政居民 | 8 | ||
| 不积极上网参政居民 | |||
| 合计 | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com