
【题目】已知数列{an}的前n项和是Sn , 且Sn+ ![]() an=1(n∈N+)
an=1(n∈N+)
(1)求数列{an}的通项公式;
(2)设bn= ![]() (1﹣Sn+1)(n∈N+),令Tn=
(1﹣Sn+1)(n∈N+),令Tn= ![]() ,求Tn .
,求Tn .
【答案】
(1)解:当n=1时,a1=S1,由 ![]() ,得:
,得: ![]() .
.
当n≥2时, ![]() .
.
则 ![]() ,即
,即 ![]() ,
,
所以 ![]() .
.
∵ ![]() ,∴
,∴ ![]() .
.
故数列{an}是以 ![]() 为首项,
为首项, ![]() 为公比的等比数列.
为公比的等比数列.
故 ![]() (n∈N*).
(n∈N*).
(2)解:∵ ![]() ,∴
,∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
所以,Tn= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)首先由递推式求出a1 , 取n=n﹣1(n≥2)得另一递推式,两式作差后可证出数列{an}是等比数列,则其通项公式可求;(2)把(1)中求出的an代入递推式,则可求出1﹣Sn+1 , 整理后得到bn , 最后利用裂项相消求Tn .
【考点精析】根据题目的已知条件,利用等差数列的通项公式(及其变式)和等比数列的通项公式(及其变式)的相关知识可以得到问题的答案,需要掌握通项公式:![]() 或
或![]() ;通项公式:
;通项公式:![]() .
.


科目:高中数学 来源: 题型:
【题目】两个非零向量 ![]() 、
、 ![]() 不共线.
不共线.
(1)若 ![]() =
= ![]() +
+ ![]() ,
, ![]() =2
=2 ![]() +8
+8 ![]() ,
, ![]() =3(
=3( ![]() ﹣
﹣ ![]() ),求证:A、B、D三点共线;
),求证:A、B、D三点共线;
(2)求实数k使k ![]() +
+ ![]() 与2
与2 ![]() +k
+k ![]() 共线.
共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我省城乡居民社会养老保险个人年缴费分100,200,300,400,500,600,700,800,900,1000(单位:元)十个档次,某社区随机抽取了50名村民,按缴费在100:500元,600:1000元,以及年龄在20:39岁,40:59岁之间进行了统计,相关数据如下:
100﹣500元 | 600﹣1000 | 总计 | |
20﹣39 | 10 | 6 | 16 |
40﹣59 | 15 | 19 | 34 |
总计 | 25 | 25 | 50 |
(1)用分层抽样的方法在缴费100:500元之间的村民中随机抽取5人,则年龄在20:39岁之间应抽取几人?
(2)在缴费100:500元之间抽取的5人中,随机选取2人进行到户走访,求这2人的年龄都在40:59岁之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆);
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() .
.
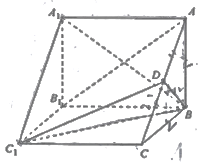
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足Sn=2n﹣an(n∈N*).
(1)计算a1 , a2 , a3 , a4 , 并由此猜想通项公式an;
(2)用数学归纳法证明(Ⅰ)中的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a3=6,a5+a7=24,{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn= ![]() (n∈N+),求数列{bn}的前n项和Tn .
(n∈N+),求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com