
已知点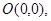
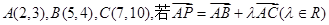
(1)是否存在 ,使得点P在第一、三象限的角平分线上?
,使得点P在第一、三象限的角平分线上?
(2)是否存在 ,使得四边形
,使得四边形 为平行四边形?(若存在,则求出
为平行四边形?(若存在,则求出 的值,若不存在,请说明理由.)
的值,若不存在,请说明理由.)
(1)存在;(2)不存在.
解析试题分析:(1)根据已知的等式求得P的坐标,再根据P在第一、三象限角平分线上可以得到P的坐标满足 ,从而可以建立关于
,从而可以建立关于 的方程,方程组的解的情况即是
的方程,方程组的解的情况即是 的存在情况;(2)由四边形OBPA是平行四边形,结合向量加法的平行四边形法则,可以得到
的存在情况;(2)由四边形OBPA是平行四边形,结合向量加法的平行四边形法则,可以得到 ,从而建立关于
,从而建立关于 的方程组,方程组的解的情况即是
的方程组,方程组的解的情况即是 的存在情况.
的存在情况.
(1)存在.
设 ,则
,则 ,∵
,∵ 3分
3分
由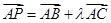 得
得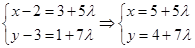 5分
5分
若点P在第一、三象限的角平分线上,则 ,即
,即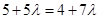 ,
, . 6分
. 6分
(2)不存在.
若四边形OBPA为平行四边形,则 8分
8分
∵ ,∴
,∴ ,方程组无解,因此满足条件的
,方程组无解,因此满足条件的 不存在 10分
不存在 10分
考点:1、向量的坐标运算;2、第一、三象限角平分线上点的坐标特点3、向量加法的平行四边形法则.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知向量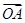 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3), =(5-m,-3-m).
=(5-m,-3-m).
(1)若点A,B,C不能构成三角形,求实数m满足的条件;
(2)若△ABC为直角三角形,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设a、b是不共线的两个非零向量,
(1)若 =2a-b,
=2a-b, =3a+b,
=3a+b,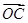 =a-3b,求证:A、B、C三点共线;
=a-3b,求证:A、B、C三点共线;
(2)若8a+kb与ka+2b共线,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知平面向量a=( ,-1),b=
,-1),b=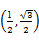 .
.
(1)若x=(t+2)a+(t2-t-5)b,y=-ka+4b(t,k∈R),且x⊥y,求出k关于t的关系式k=f(t).
(2)求函数k=f(t)在t∈(-2,2)上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知复平面内平行四边形ABCD(A,B,C,D按逆时针排列),A点对应的复数为2+i,向量 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i.
对应的复数为3-i.
(1)求点C,D对应的复数.
(2)求平行四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线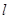 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.
(1)求点P的轨迹方程;
(2)是否存在定直线 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com