
【题目】[选修4一4:坐标系与参数方程]已知直线l过原点且倾斜角为![]() ,
, ![]()
![]()
![]() ,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为psin
,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为psin![]()
![]() =4cos
=4cos![]() .
.
(I)写出直线l的极坐标方程和曲线C 的直角坐标方程;
(Ⅱ)已知直线l过原点且与直线l相互垂直,若l![]() C=-M,l
C=-M,l![]() C=N,其中M,N不与原点重合,求△OMN 面积的最小值.
C=N,其中M,N不与原点重合,求△OMN 面积的最小值.
【答案】(1)![]() =
=![]() ,y
,y![]() =4x.(2)16
=4x.(2)16
【解析】试题分析:(1)根据极角定义得直线l的极坐标方程,根据![]() 将曲线C 的极坐标方程化为直角坐标方程;(2)先确定直线
将曲线C 的极坐标方程化为直角坐标方程;(2)先确定直线![]() 极坐标方程,代入求得
极坐标方程,代入求得![]() ,根据面积公式可得S,最后根据三角函数有界性求最小值.
,根据面积公式可得S,最后根据三角函数有界性求最小值.
试题解析:解:(I)依题意,直线l的极坐标方程为![]() =
=![]() (
(![]() ≠
≠![]() ,
, ![]() ∈R)
∈R)
曲线C: ![]() Sin
Sin![]()
![]() =4cos
=4cos![]() ,
,![]() sin
sin ![]() =4
=4![]() cos
cos![]() ,直角坐标方程为y
,直角坐标方程为y![]() =4x.
=4x.
(Ⅱ)把θ=![]() 代入
代入![]() sin
sin ![]() =4cos
=4cos![]() ,得
,得![]() =
=![]() .
.
可知直线l的极坐标方程为![]() =
=![]() +
+![]() (
(![]() ∈R)
∈R)
代入![]() sin
sin![]()
![]() =4cos
=4cos![]() ,得
,得![]() cos
cos ![]() =-4sin
=-4sin![]() ,所以
,所以![]() =-
=-![]() ,
,
S△![]() =
=![]() |OM|·|ON|=2|
|OM|·|ON|=2|![]() |·|
|·|![]() |=
|=![]() ≥16,(当且仅当
≥16,(当且仅当![]() =
=![]() 时,取“=”)
时,取“=”)
即△OMN面积的最小值为16.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,一条准线方程为
,一条准线方程为![]() 过椭圆的上顶点A作一条与x轴、y轴都不垂直的直线交椭圆于另一点P,P关于x轴的对称点为Q.
过椭圆的上顶点A作一条与x轴、y轴都不垂直的直线交椭圆于另一点P,P关于x轴的对称点为Q.
![]() 求椭圆的方程;
求椭圆的方程;
![]() 若直线AP,AQ与x轴交点的横坐标分别为m,n,求证:mn为常数,并求出此常数.
若直线AP,AQ与x轴交点的横坐标分别为m,n,求证:mn为常数,并求出此常数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆70周年庆典磅礴而又欢快的场景,仍历历在目.已知庆典中某省的游行花车需要用到某类花卉,而该类花卉有甲、乙两个品种,花车的设计团队对这两个品种进行了检测.现从两个品种中各抽测了10株的高度,得到如下茎叶图.下列描述正确的是( )

A.甲品种的平均高度大于乙品种的平均高度,且甲品种比乙品种长的整齐
B.甲品种的平均高度大于乙品种的平均高度,但乙品种比甲品种长的整齐
C.乙品种的平均高度大于甲品种的平均高度,且乙品种比甲品种长的整齐
D.乙品种的平均高度大于甲品种的平均高度,但甲品种比乙品种长的整齐
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(e![]() +1)
+1)
(I)求函数y=f(x)的图象在点(0,f(0))处的切线方程;
(II)若函数g(x)=f(x)-ae![]() -x,求函数g(x)在[1,2]上的最大值。
-x,求函数g(x)在[1,2]上的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为缓减人口老年化带来的问题,中国政府在2016年1月1日作出全国统一实施全面的“二孩”政策,生“二孩”是目前中国比较流行的元素![]() 某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”
某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”![]() 现已得知100人中同意父母生“二孩”占
现已得知100人中同意父母生“二孩”占![]() ,统计情况如表:
,统计情况如表:
性别属性 | 同意父母生“二孩” | 反对父母生“二孩” | 合计 |
男生 | 10 | ||
女生 | 30 | ||
合计 | 100 |
![]() 请补充完整上述列联表;
请补充完整上述列联表;
![]() 根据以上资料你是否有
根据以上资料你是否有![]() 把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
参考公式与数据:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某公司生产的商品A每件售价为5元时,年销售10万件,
(1)据市场调查,若价格每提高一元,销量相应减少1万件,要使销售收入不低于原销售收入,该商品的销售价格最多提高多少元?
(2)为了扩大该商品的影响力,公司决定对该商品的生产进行技术革新,将技术革新后生产的商品售价提高到每件![]() 元,公司拟投入
元,公司拟投入![]() 万元作为技改费用,投入
万元作为技改费用,投入![]() 万元作为宣传费用。试问:技术革新后生产的该商品销售量m至少应达到多少万件时,才可能使技术革新后的该商品销售收入等于原销售收入与总投入之和?
万元作为宣传费用。试问:技术革新后生产的该商品销售量m至少应达到多少万件时,才可能使技术革新后的该商品销售收入等于原销售收入与总投入之和?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是首项为a,公差为d的等差数列(d≠0),
是首项为a,公差为d的等差数列(d≠0), ![]() 是其前n项的和.记
是其前n项的和.记![]() ,n∈N*,其中c为实数.
,n∈N*,其中c为实数.
(1)若c=0,且b1,b2,b4成等比数列,证明:Snk=n2Sk(k,n∈N*);
(2)若{![]() }是等差数列,证明:c=0.
}是等差数列,证明:c=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机和电子阅读器越来越普及,人们的阅读习惯也发生了改变,手机和电子阅读产品方便易携带,越来越多的人习惯通过手机或电子阅读器阅读.某电子书阅读器厂商随机调查了![]() 人,统计了这
人,统计了这![]() 人每日平均通过手机或电子阅读器阅读的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知阅读时间在
人每日平均通过手机或电子阅读器阅读的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知阅读时间在![]() ,
, ![]() ,
, ![]() 三组对应的人数依次成等差数列.
三组对应的人数依次成等差数列.
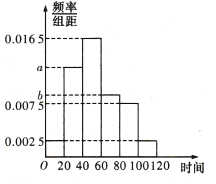
(1)求频率分布直方图中![]() ,
, ![]() 的值;
的值;
(2)若将日平均阅读时间不少于![]() 分钟的用户定义为“电子阅读发烧友”,将日平均阅读时间少于
分钟的用户定义为“电子阅读发烧友”,将日平均阅读时间少于![]() 分钟的用户定义为“电子阅读潜在爱好者”,现从上述“电子阅读发烧友”与“电子阅读潜在爱好者”的人中按分层抽样选出
分钟的用户定义为“电子阅读潜在爱好者”,现从上述“电子阅读发烧友”与“电子阅读潜在爱好者”的人中按分层抽样选出![]() 人,再从这
人,再从这![]() 人中任取
人中任取![]() 人,求恰有
人,求恰有![]() 人为“电子阅读发烧友”的概率.
人为“电子阅读发烧友”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com