
【题目】已知函数f(x)=x(e![]() +1)
+1)
(I)求函数y=f(x)的图象在点(0,f(0))处的切线方程;
(II)若函数g(x)=f(x)-ae![]() -x,求函数g(x)在[1,2]上的最大值。
-x,求函数g(x)在[1,2]上的最大值。
【答案】(1)y=2x(2)见解析
【解析】试题分析:(1)先根据导数几何意义求切线斜率,再根据点斜式得切线方程,(2)先求导数,再求导函数零点,根据零点与定义区间相对位置关系确定函数单调性,最后根据单调性确定函数最大值取法.
试题解析:解:(I)依题意,f(x)=e![]() +1+xe
+1+xe![]() ,故f(0)=e
,故f(0)=e![]() +1=2.
+1=2.
因为f(0)=0,故所求切线方程为y=2x;.
(Ⅱ)依题意,g(x)=(x-a+1)·e![]() ,令g(x)=0得x=a-1
,令g(x)=0得x=a-1
所以当a-1≤1时,x∈[1,2]时,g(x)≥0恒成立,g(x)单调递增,g(x)最大值为g(2),.
当a-1≥2时,x∈[1,2]时,g(x)≤0恒成立,g(x)单调递减,g(x)最大值为g(1).
当1<a-1<2时,x∈[1,a-1)时,g(x)≤0,g(x)单调递减;
x∈(a-1,2)时,g(x)>0,g(x)单调递增.
当x∈[1,2]时,g(x)最大值为g(1)或g(2).
g(1)=(1-a)e,g(2)=(2-a)e![]() ,
,
g(1)-g(2)=(1-a)e-(2-a)e![]() =(e
=(e![]() -e)a-(2e
-e)a-(2e![]() -e).
-e).
∴当![]() 时,g(1)-g(2)≥0,g(x)max=g(1)=(1-a)e.
时,g(1)-g(2)≥0,g(x)max=g(1)=(1-a)e.
当a<![]() =
=![]() 时,g(1)-g(2)<0,g(x)max=g(2)=(2-a)e
时,g(1)-g(2)<0,g(x)max=g(2)=(2-a)e![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】对于给定的正整数![]() ,若数列
,若数列![]() 满足
满足![]() 对任意正整数
对任意正整数![]() 总成立,则称数列
总成立,则称数列![]() 是“
是“![]() 数列”.
数列”.
(1)证明:等差数列![]() 是“
是“![]() 数列”;
数列”;
(2)若数列![]() 既是“
既是“![]() 数列”,又是“
数列”,又是“![]() 数列”,证明:
数列”,证明: ![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知在四棱锥![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.
的中点.
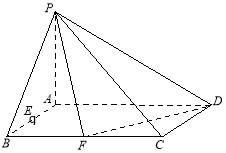
(1)判断并说明![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不
的值;若不
存在,请说明理由;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标坐标系![]() 中,过点P(1,0)的直线l的参数方程为
中,过点P(1,0)的直线l的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知顶点在极轴上,开口向右的抛物线C经过极坐标为(2,
轴的正半轴为极轴建立极坐标系,已知顶点在极轴上,开口向右的抛物线C经过极坐标为(2, ![]() )的点Q.
)的点Q.
(1)求C的极坐标方程;
(2)若l与C交于A、B两点,且|PA|=2|PB|,求tan![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ADEF与梯形ABCD所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,M为CE的中点,N为CD中点.
,M为CE的中点,N为CD中点.
![]() 求证:平面
求证:平面![]() 平面ADEF;
平面ADEF;
![]() 求证:平面
求证:平面![]() 平面BDE;
平面BDE;
![]() 求点D到平面BEC的距离.
求点D到平面BEC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4一4:坐标系与参数方程]已知直线l过原点且倾斜角为![]() ,
, ![]()
![]()
![]() ,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为psin
,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为psin![]()
![]() =4cos
=4cos![]() .
.
(I)写出直线l的极坐标方程和曲线C 的直角坐标方程;
(Ⅱ)已知直线l过原点且与直线l相互垂直,若l![]() C=-M,l
C=-M,l![]() C=N,其中M,N不与原点重合,求△OMN 面积的最小值.
C=N,其中M,N不与原点重合,求△OMN 面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某集团为了获得更大的收益,每年要投入一定的资金用于广告促销.经调查投入广告费t(百万元),可增加销售额约为-t2+5t(百万元)(0≤t≤5) (注:收益=销售额-投放).
(1)若该公司将当年的广告费控制在3百万元之内,则应投入多少广告费,才能使该公司由此获得的收益最大?
(2)现该公司准备共投入3百万元,分别用于广告促销和技术改造.经预测,每投入技术改造费x(百万元),可增加的销售额约为-![]() x3+x2+3x(百万元).请设计一个资金分配方案,使该公司由此获得的收益最大.
x3+x2+3x(百万元).请设计一个资金分配方案,使该公司由此获得的收益最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一年来,某足球队的![]() 足球运动员每天进行距离球门
足球运动员每天进行距离球门![]() 米远的射门训练
米远的射门训练![]() 次,若打进球门算成功,否则算失败.随机提取该球员连续
次,若打进球门算成功,否则算失败.随机提取该球员连续![]() 天的成功次数统计如下:
天的成功次数统计如下:
![]() .
.
(1)估计该球员一天射门成功次数的四分位数;
(2)若每天![]() 三位球员均进行“三角战术”配合训练,要求三位球员在运动中必须保持如下规则:三人所在的位置构成
三位球员均进行“三角战术”配合训练,要求三位球员在运动中必须保持如下规则:三人所在的位置构成![]() ,
,![]() ,
,![]() 的面积
的面积![]() (平方米).求
(平方米).求![]() 球员之间的距离的最小值(米).
球员之间的距离的最小值(米).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现安排甲、乙、丙、丁、戊5名同学参加2022年杭州亚运会志愿者服务活动,有翻译、导游、礼仪、司机四项工作可以安排,以下说法正确的是( )
A. 每人都安排一项工作的不同方法数为![]()
B. 每项工作至少有一人参加,则不同的方法数为![]()
C. 如果司机工作不安排,其余三项工作至少安排一人,则这5名同学全部被安排的不同方法数为![]()
D. 每项工作至少有一人参加,甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com