
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() ,并且函数
,并且函数![]() 在实数集
在实数集![]() 上是单调增函数,求实数
上是单调增函数,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,
,![]() ,
,![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(3)若![]() ,
,![]() 都不为0,记函数
都不为0,记函数![]() 的图象为曲线
的图象为曲线![]() ,设点
,设点![]() ,
,![]() 是曲线
是曲线![]() 上的不同两点,点
上的不同两点,点![]() 为线段
为线段![]() 的中点,过点
的中点,过点![]() 作
作![]() 轴的垂线交曲线
轴的垂线交曲线![]() 于点
于点![]() .试问:曲线
.试问:曲线![]() 在点
在点![]() 处的切线是否平行于直线
处的切线是否平行于直线![]() ?并说明理由.
?并说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 的值域是
的值域是![]() ,当
,当![]() 的值域是
的值域是![]() ,当
,当![]() 的值域是
的值域是![]() ;(3)曲线
;(3)曲线![]() 在点
在点![]() 处的切线不平行于直线
处的切线不平行于直线![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)只需![]() 在
在![]() 上恒成立,根据二次函数根的判别式,即可求解;
上恒成立,根据二次函数根的判别式,即可求解;
(2)求导,对![]() 分类讨论,求出
分类讨论,求出![]() 在
在![]() 单调性,进而求出极值最值,即可得出结论;
单调性,进而求出极值最值,即可得出结论;
(3)由已知得到![]() 点坐标,由两点式求出
点坐标,由两点式求出![]() 的斜率,再由导数得到曲线
的斜率,再由导数得到曲线![]() 在
在![]() 处的斜率,由斜率相等,设
处的斜率,由斜率相等,设![]() ,得到
,得到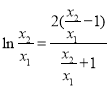 ,令
,令![]() ,后构造函数
,后构造函数![]() ,判断
,判断![]() 是否存在零点,即可得出结论.
是否存在零点,即可得出结论.
(1)![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 函数
函数![]() 在实数集
在实数集![]() 上是单调增函数,
上是单调增函数,
![]() 在
在![]() 上恒成立,
上恒成立,
![]() ,
,
实数![]() 的取值范围
的取值范围![]() ;
;
(2)当![]() ,
,![]() ,
,![]() 时,
时,![]()
![]() ,
,
当![]() ,
,
![]() 单调递增,
单调递增,
![]() 单调递减,
单调递减,
当![]() ,
,![]() ,
,
![]()
![]() ,当
,当![]() ,
,
![]() ,
,
当![]() ,
,
综上,当![]() 的值域是
的值域是![]() ,
,
当![]() 的值域是
的值域是![]() ,
,
当![]() 的值域是
的值域是![]() ;
;
(3)![]() ,
,![]() 都不为0时,
都不为0时,![]() 点横坐标为
点横坐标为![]()
函数![]() ,
,
![]() ,曲线在
,曲线在![]() 处的切线斜率为
处的切线斜率为
![]()
![]() ,
,
直线![]() 的斜率为
的斜率为![]() ,
,
则![]()
![]() ,
,
假设曲线![]() 在点
在点![]() 处的切线平行于直线
处的切线平行于直线![]() ,则
,则![]() ,
,
即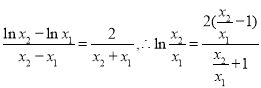 ,
,
不妨设![]() ,则
,则![]() ,
,
令![]() ,
,
![]() 时恒成立,
时恒成立,
所以![]() 在
在![]() 上是增函数,又
上是增函数,又![]() ,
,
![]() ,即
,即![]() 在
在![]() 上不成立,
上不成立,
![]() 曲线
曲线![]() 在点
在点![]() 处的切线不平行直线
处的切线不平行直线![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 、
、![]() 、
、![]() 都有
都有![]() ,满足
,满足![]() 的实数
的实数![]() 有且只有3个,给出下述四个结论:①满足题目条件的实数
有且只有3个,给出下述四个结论:①满足题目条件的实数![]() 有且只有2个:②满足题目条件的实数
有且只有2个:②满足题目条件的实数![]() 有且只有2个;③
有且只有2个;③![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的取值范围是
的取值范围是![]() .其中所有正确的个数是( )
.其中所有正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程选讲
在平面直角坐标系中,以原点为极点,以![]() 轴非负半轴为极轴建立极坐标系, 已知曲线
轴非负半轴为极轴建立极坐标系, 已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 过点
过点![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】石嘴山市第三中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示:
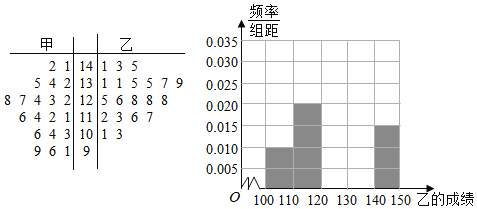
(1)根据茎叶图求甲乙两位同学成绩的中位数,并将同学乙的成绩的频率分布直方图填充完整;
(2)根据茎叶图比较甲乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可);
(3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,记事件![]() 为“其中2个成绩分别属于不同的同学”,求事件
为“其中2个成绩分别属于不同的同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 点关于原点
点关于原点![]() 对称的点为
对称的点为![]() 二次函数
二次函数![]() 的图像经过点
的图像经过点![]() 和点
和点![]() 回答以下问题:
回答以下问题:
(1)用![]() 表示
表示![]() 和
和![]() 的图像的顶点的纵坐标;
的图像的顶点的纵坐标;
(2)证明:若二次函数![]() 的图像上的点
的图像上的点![]() 满足
满足![]() ,则向量
,则向量![]() 与
与![]() 的数量积大于
的数量积大于![]() .
.
(3)当变![]() 化时,求
化时,求![]() 中二次函数顶点纵坐标
中二次函数顶点纵坐标![]() 的最大值,并求出此时
的最大值,并求出此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
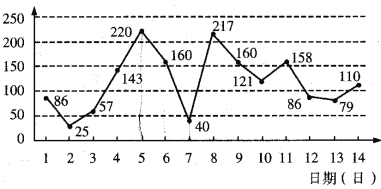
【题目】下图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表.某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
空气质量指数 | 污染程度 |
小于100 | 优良 |
大于100且小于150 | 轻度 |
大于150且小于200 | 中度 |
大于200且小于300 | 重度 |
(1)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(2)求此人到达当日空气质量优良的概率;
(3)求此人出差期间(两天)空气质量至少有一天为中度或重度污染的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com