
【题目】某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.
(1)求该校报名学生的总人数;
(2)从报名的学生中任选3人,设X表示体重超过60kg的学生人数,求X的数学期望.
【答案】解:(1)∵从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.
∴从左到右3个小组的频数分别为6,12,18,共有36人,
第4,5小组的频率之和为(0.0375+0.0125)×5=0.25,
则前3小组的频率之和为1﹣0.25=0.75,
则该校报名学生的总人数为36÷0.75=48;
(2)第4,5小组的频数为48×0.25=12,
则体重超过60kg的学生人数为12+18=30,
则X=0,1,2,3,
则P(X=0)=![]() =
=![]() ≈0.047,P(X=1)=
≈0.047,P(X=1)=![]() =≈0.265,
=≈0.265,
P(X=2)=![]() ≈0.453,P(X=3)=
≈0.453,P(X=3)=![]() =
=![]() ≈0.235,
≈0.235,
则EX=0×0.047+1×0.265+2×0.453+3×0.235=1.876,
即X的数学期望EX=1.876
【解析】(1)根据频数关系求出每段的频数即可求该校报名学生的总人数;
(2)X=0,1,2,3,求出每个变量对应的概率,即可得到结论.
【考点精析】根据题目的已知条件,利用频率分布直方图的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且经过点
,且经过点![]() ,直线
,直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() .
.
(1)求椭圆的方程;
(2)求![]() 的取值范围;
的取值范围;
(3)若直线![]() 不过点
不过点![]() ,求证:直线
,求证:直线![]() 的斜率互为相反数.
的斜率互为相反数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x-a|+x,其中a>0.
(1)当a=3时,求不等式f(x)≥x+4的解集;
(2)若不等式f(x)≥x+2a2在x∈[1,3]恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的方程(x﹣1)4+mx﹣m﹣2=0各个实根x1 , x2…xk(k≤4,k∈N*)所对应的点(xi![]() ),(i=1,2,3…k)均在直线y=x的同侧,则实数m的取值范围是( )
),(i=1,2,3…k)均在直线y=x的同侧,则实数m的取值范围是( )
A.(﹣1,7)
B.(﹣∞,﹣7)U(﹣1,+∞)
C.(﹣7,1)
D.(﹣∞,1)U(7,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某公路![]() 一侧有一块空地
一侧有一块空地![]() ,其中
,其中 ![]() ,
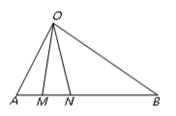
,![]() .当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
.当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
(1)若M在距离A点2 km处,求点M,N之间的距离;
(2)为节省投入资金,人工湖△OMN的面积要尽可能小.试确定M的位置,使△OMN的面积最小,并求出最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(
=(![]() sin x,cos x),
sin x,cos x),![]() =(cos x,cos x),
=(cos x,cos x),![]() =(2
=(2![]() ,1).
,1).
(1)若![]() ∥
∥![]() ,求sin xcos x的值;
,求sin xcos x的值;
(2)若0<x≤![]() ,求函数f(x)=
,求函数f(x)=![]() ·
·![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北方某市一次全市高中女生身高统计调查数据显示:全市20000名高中女生的身高(单位:![]() )服从正态分布
)服从正态分布![]() .现从某高中女生中随机抽取50名测量身高,测量发现被测学生身高全部在
.现从某高中女生中随机抽取50名测量身高,测量发现被测学生身高全部在![]() 和
和![]() 之间,现将测量结果按如下方式分成6组:第1组
之间,现将测量结果按如下方式分成6组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.

(1)求这50名女生身高不低于172![]() 的人数;
的人数;
(2)在这50名女生身高不低于172![]() 的人中任意抽取2人,将该2人中身高排名(从高到低)在全市前260名的人数记为
的人中任意抽取2人,将该2人中身高排名(从高到低)在全市前260名的人数记为![]() ,求
,求![]() 的数学期望.
的数学期望.
参数数据:![]() ,
,
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com