
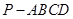 中,底面
中,底面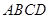 为矩形,侧棱
为矩形,侧棱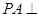 底面
底面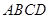 ,
,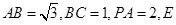 为
为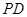 的中点.
的中点.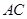 与
与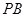 所成角的余弦值;
所成角的余弦值;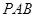 内找一点
内找一点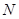 ,使
,使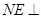 平面
平面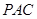 ,并分别求出点
,并分别求出点 到
到 和
和 的距离.
的距离.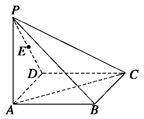
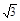 ,0,0)、C(
,0,0)、C(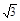 ,1,0)、D(0,1,0)、P(0,0,2)、
,1,0)、D(0,1,0)、P(0,0,2)、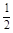 ,1),从而
,1),从而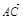 =(
=(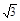 ,1,0),
,1,0),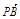 =(
=(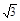 ,0,-2).
,0,-2).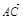 与
与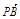 的夹角为
的夹角为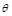 ,则cos
,则cos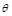 =
= =
=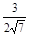 =
=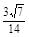 ,
,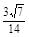 ……………………………………7分
……………………………………7分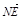 =(-x,
=(-x,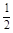 ,1-z),由NE⊥平面PAC可得
,1-z),由NE⊥平面PAC可得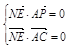 ,即
,即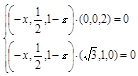 ,化简得
,化简得 ,∴
,∴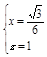
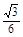 ,0,1),
,0,1),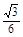 …………………14分
…………………14分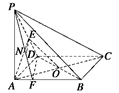
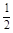 PB=
PB=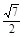 ,AE=
,AE=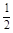 PD=
PD=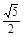 ,
,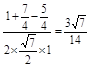 ,
,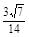 .
.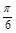 .连接PF,则在Rt△ADF中,DF=
.连接PF,则在Rt△ADF中,DF=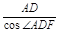 =
=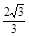 ,AF=AD·tan∠ADF=
,AF=AD·tan∠ADF=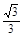 .
.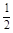 AP=1,N点到AP的距离为
AP=1,N点到AP的距离为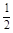 AF=
AF=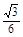 .
.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源:不详 题型:单选题
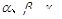 表示三个不同的平面,有下列四个命题:
表示三个不同的平面,有下列四个命题: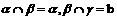 且
且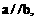 则
则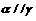 ;
;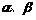 外,
外,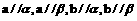 ,则
,则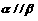 ;
;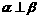 ,
,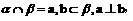 则
则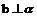 ;
;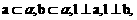 则
则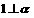 .
.| A.①② | B.②③ |
| C.①④ | D.③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
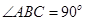 ,AD=a,BC=2a,
,AD=a,BC=2a,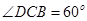 ,在平面ABCD内,过C作
,在平面ABCD内,过C作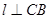 ,以
,以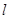 为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积。
为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积。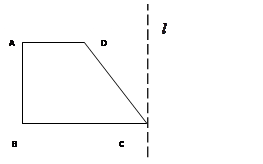
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
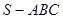 中,
中, 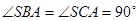 , △
, △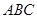 是斜边
是斜边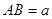 的等腰直角三角形, 则以下结论中: ① 异面直线
的等腰直角三角形, 则以下结论中: ① 异面直线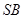 与
与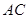 所成的角为
所成的角为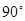 ; ② 直线
; ② 直线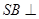 平面
平面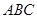 ; ③ 面
; ③ 面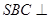 面
面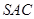 ; ④ 点
; ④ 点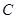 到平面
到平面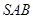 的距离是
的距离是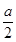 . 其中正确结论的序号是 ______
. 其中正确结论的序号是 ______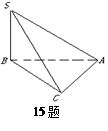
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com