
【题目】如图,三棱柱![]() 中,侧棱垂直于底面,
中,侧棱垂直于底面,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
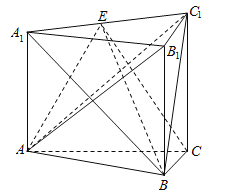
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)设平面![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长
的长
【答案】(Ⅰ)见证明;(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
(Ⅰ)证明![]() 平面
平面![]() .推出
.推出![]() .然后证明
.然后证明![]() 平面
平面![]() .得到
.得到![]() .
.![]() .即可证明
.即可证明![]() 平面
平面![]() .
.
(Ⅱ)说明![]() .证明
.证明![]() 平面
平面![]() .通过
.通过![]() 求解即可.
求解即可.
(Ⅲ)证明![]() .说明
.说明![]() 为
为![]() 中点.然后求解即可.
中点.然后求解即可.
解:(Ⅰ)因为三棱柱![]() 中,
中,
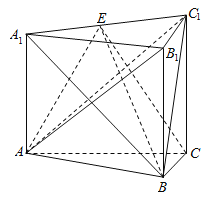
侧棱垂直于底面,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() .
.
因为![]() ,所以四边形
,所以四边形![]() 为菱形.
为菱形.
所以![]() .
.
因为![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)由已知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .
.
因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() ,故
,故![]() 到平面
到平面![]() 的距离为2.
的距离为2.
因为![]() 为
为![]() 中点,所以
中点,所以![]() 点到平面
点到平面![]() 距离为1.
距离为1.
所以![]()
(Ⅲ)在三棱柱![]() 中,
中,

因为![]() ,
,![]() 为平面
为平面![]() 与平面
与平面![]() 的公共点,
的公共点,
所以平面![]() 平面
平面![]() .
.
因为平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又平面![]() 平面
平面![]() ,
,
所以![]() .
.
又![]() ,所以
,所以![]() .
.
因为![]() 为
为![]() 中点,所以
中点,所以![]() 为
为![]() 中点.
中点.
所以![]()


科目:高中数学 来源: 题型:
【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7, 8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了 20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司研发了两种具有自主知识产权的操作系统,分别命名为“天下”、“东方”.这两套操作系统均适用于手机、电脑、车联网、物联网等,且较国际同类操作系统更加流畅.
(1)为了解喜欢“天下”系统是否与性别有关,随机调查了![]() 名男用户和
名男用户和![]() 名女用户,每位用户对“天下”系统给出喜欢或不喜欢的评价,得到下面列联表:
名女用户,每位用户对“天下”系统给出喜欢或不喜欢的评价,得到下面列联表:

请问:能否有![]() 的把握认为男、女用户对“天下”系统的喜欢有差异?
的把握认为男、女用户对“天下”系统的喜欢有差异?
附: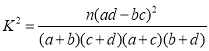 .
.

(2)该公司选定![]() 万名用户对“天下”和“东方”操作系统(以下简称“天下”、“东方”)进行测试,每个用户只能从“天下”或“东方”中选择一个使用,每经过一个月后就给用户一次重新选择“天下”或“东方”的机会.这个月选择“天下”的用户在下个月选择“天下”的概率均为
万名用户对“天下”和“东方”操作系统(以下简称“天下”、“东方”)进行测试,每个用户只能从“天下”或“东方”中选择一个使用,每经过一个月后就给用户一次重新选择“天下”或“东方”的机会.这个月选择“天下”的用户在下个月选择“天下”的概率均为![]() ,选择“东方”的概率均为
,选择“东方”的概率均为![]() ,
,![]() ;这个月选择“东方”的用户在下个月选择“天下”的概率均为
;这个月选择“东方”的用户在下个月选择“天下”的概率均为![]() ,选择“东方”的概率均为
,选择“东方”的概率均为![]() ,
,![]() .记
.记![]() 表示第
表示第![]() 个月用户选择“天下”的概率,已知
个月用户选择“天下”的概率,已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(ⅰ)求![]() 的值;
的值;
(ⅱ)证明:数列![]() (
(![]() )为等比数列;
)为等比数列;
(ⅲ)预测选择“天下”操作系统的用户数量不超过多少万人.(精确到1万)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 轴、
轴、![]() 轴正方向的单位向量分别为
轴正方向的单位向量分别为![]() ,坐标平面上的点
,坐标平面上的点![]() 满足条件:
满足条件:![]() ,
,![]()
![]() .
.
(1)若数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
(2)求向量![]() 的坐标,若
的坐标,若![]() 的面积
的面积![]() 构成数列
构成数列![]() ,写出数列
,写出数列![]() 的通项公式.
的通项公式.
(3)若![]() ,指出
,指出![]() 为何值时,
为何值时,![]() 取得最大值,并说明理由.
取得最大值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一![]() 班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

![]() 1
1![]() 求分数在
求分数在![]() 的频数及全班人数;
的频数及全班人数;
![]() 2
2![]() 求分数在
求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
![]() 3
3![]() 若要从分数在
若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的.如图,椭圆![]() 与椭圆
与椭圆![]() 是相似的两个椭圆,并且相交于上下两个顶点,椭圆
是相似的两个椭圆,并且相交于上下两个顶点,椭圆![]() 的长轴长是4,椭圆
的长轴长是4,椭圆![]() 长轴长是2,点
长轴长是2,点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左焦点与右焦点.
的左焦点与右焦点.

(1)求椭圆![]() ,
,![]() 的方程;
的方程;
(2)过![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
,![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某商品每件的生产成本![]() (元)与销售价格
(元)与销售价格![]() (元)具有线性相关关系,对应数据如表所示:
(元)具有线性相关关系,对应数据如表所示:
| 5 | 6 | 7 | 8 |
| 15 | 17 | 21 | 27 |
(1)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该商品的月销售量![]() (千件)与生产成本
(千件)与生产成本![]() (元)的关系为
(元)的关系为![]() ,
,![]() ,根据(1)中求出的线性回归方程,预测当
,根据(1)中求出的线性回归方程,预测当![]() 为何值时,该商品的月销售额最大.
为何值时,该商品的月销售额最大.
附: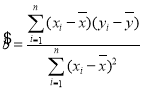 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 是长轴的一个端点,弦
是长轴的一个端点,弦![]() 过椭圆的中心
过椭圆的中心![]() ,点
,点![]() 在第一象限,且
在第一象限,且![]() ,
,![]() .
.
(1)求椭圆的标准方程;
(2)设![]() 、
、![]() 为椭圆上不重合的两点且异于
为椭圆上不重合的两点且异于![]() 、
、![]() ,若
,若![]() 的平分线总是垂直于
的平分线总是垂直于![]() 轴,问是否存在实数
轴,问是否存在实数![]() ,使得
,使得![]() ?若不存在,请说明理由;若存在,求
?若不存在,请说明理由;若存在,求![]() 取得最大值时的
取得最大值时的![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com