
【题目】设![]() 轴、
轴、![]() 轴正方向的单位向量分别为
轴正方向的单位向量分别为![]() ,坐标平面上的点
,坐标平面上的点![]() 满足条件:
满足条件:![]() ,
,![]()
![]() .
.
(1)若数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
(2)求向量![]() 的坐标,若
的坐标,若![]() 的面积
的面积![]() 构成数列
构成数列![]() ,写出数列
,写出数列![]() 的通项公式.
的通项公式.
(3)若![]() ,指出
,指出![]() 为何值时,
为何值时,![]() 取得最大值,并说明理由.
取得最大值,并说明理由.
【答案】![]()
![]()
![]() ;
;![]()
![]() ;
;![]() 当
当![]() 或
或![]() 时,
时,![]() 取得最大值为
取得最大值为![]() .
.
【解析】
(1)运用平面向量数量积的坐标表示,结合平面向量垂直的条件,可得![]() ,再由
,再由![]() 与
与![]() 的关系,即可求得数列
的关系,即可求得数列![]() 的通项公式;
的通项公式;
(2)运用平面向量的多边形法则,以及等比数列的求和公式,得到![]() 的坐标,再由三角形的面积公式即可得到
的坐标,再由三角形的面积公式即可得到![]() 的面积,即为数列
的面积,即为数列![]() 的通项公式;
的通项公式;
(3)利用增减数列的定义,通过判断![]() 的符号,判断数列
的符号,判断数列![]() 的单调性,即可求数列
的单调性,即可求数列![]() 最大值.
最大值.
![]() 由题意知,
由题意知, ![]() ,
,![]()
因为![]() ,
,![]() ,
,
所以![]() ①,所以当
①,所以当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ②,
②,
由①-②得:![]() ,
,
又当![]() 时,
时,![]() 符合题意,所以
符合题意,所以![]()
![]() ;
;![]() 因为
因为![]()
![]()
![]()
![]() ,
,
所以![]() ,
,
由当![]() 时,
时,![]() 的顶点坐标分别为:
的顶点坐标分别为:![]()
![]()
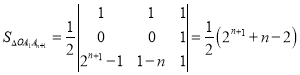
![]() ,
,
所以![]() ;
;![]() 因为
因为![]() ,由
,由![]()
![]() 知,
知,![]()
![]() ,
,
所以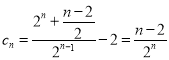 ,
,
当![]() 时,,,
时,,,
∴当![]() 时,数列
时,数列![]() 是递增数列,
是递增数列,![]() 时,数列
时,数列![]() 是递减数列,
是递减数列,
即![]()
∴当![]() 或
或![]() 时,
时,![]() 取得最大值为
取得最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
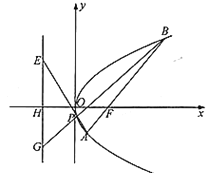
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,过
,过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 在
在![]() 轴的上方,且点
轴的上方,且点![]() 的横坐标为4.
的横坐标为4.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)设点![]() 为抛物线
为抛物线![]() 上异于
上异于![]() ,
,![]() 的点,直线
的点,直线![]() 与
与![]() 分别交抛物线
分别交抛物线![]() 的准线于
的准线于![]() ,
,![]() 两点,
两点,![]() 轴与准线的交点为
轴与准线的交点为![]() ,求证:
,求证:![]() 为定值,并求出定值.
为定值,并求出定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某分公司经销某种品牌产品,每件产品的成本为30元,并且每件产品须向总公司缴纳![]() 元(
元(![]() 为常数,
为常数,![]() )的管理费.根据多年的统计经验,预计当每件产品的售价为
)的管理费.根据多年的统计经验,预计当每件产品的售价为![]() 元时,产品一年的销售量为
元时,产品一年的销售量为![]() 为自然对数的底数)万件.已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价
为自然对数的底数)万件.已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价![]() 最低不低于35元,最高不超过41元.
最低不低于35元,最高不超过41元.
(Ⅰ)求分公司经营该产品一年的利润![]() 万元与每件产品的售价
万元与每件产品的售价![]() 元的函数关系式;
元的函数关系式;
(Ⅱ)当每件产品的售价为多少元时,该产品一年的利润![]() 最大,并求
最大,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据史载知,新华网:北京2008年11月9日电,国务院总理温家宝主持召开国务院常务会议.研究部署进一步扩大内需促进经济平稳较快增长的措施,以应对日趋严峻的全球性世界经济金融危机,在提高城乡居民特别是低收入人群的收入水平政策措施的刺激下,某零售店当时近5个月的销售额和利润额数据统计如下表:
月份 | 2 | 3 | 4 | 5 | 6 |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)若x与y之间是线性相关关系,求利润额y关于销售额x的线性回归方程![]() ;
;
(2)若9月份的销售额为8千万元,试利用(1)的结论估计该零售店9月份的利润额.
参考公式: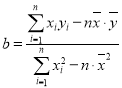 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com