
某校兴趣小组进行了一项“娱乐与年龄关系”的调查,对 15~65岁的人群随机抽取1000人的样本,进行了一次“是否是电影明星追星族”调查,得到如下各年龄段样本人数频率分布直方图和“追星族”统计表:
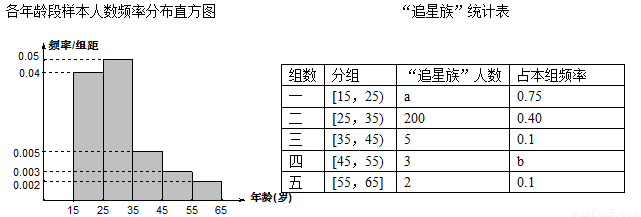
(1)求 的值.
的值.
(2)设从45岁到65岁的人群中,随机抽取2人,用样本数据估计总体, 表示其中“追星族”的人数,求
表示其中“追星族”的人数,求 分布列、期望和方差.
分布列、期望和方差.
(1)300;0.1;(2)见解析
【解析】
试题分析:(1)先由频率分布直方图计算出在[15,25]年龄段的样本人数,再根据“追星族”统计表即可计算出该段追星人数a;先由频率分布直方图计算出在[45,55]年龄段的样本人数,再由“追星族”统计表知该组“追星族”人数为3,3除以该组样本人数即为占本组的频率;(2)由[45,65]范围内样本数据即可求出抽到“追星族”的概率,由二项分布知识知,在该组中随机抽2人,抽到“追星族”的人数符合二项分布,由二项分布即可写出分布列,计算出期望与方查.
试题解析:(1)由题设知[15,25)这组人数为0.04×10×1000=400, 1分
故a=0.75×400=300 2分
[45,55)这组人数为0.003×10×1000=30,故b=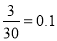 3分
3分
综上,a=300,b=0.1. 4分
(2).由[45,65]范围内的样本数据知,抽到追星族的概率为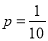
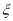 ~B(2,
~B(2,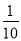 ) 6分
) 6分
故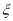 的分布列是
的分布列是
ξ | 0 | 1 | 2 |
p | 0.81 | 0.18 | 0.01 |
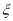 的期望是
的期望是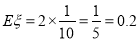 10分
10分
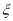 的方差是
的方差是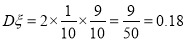 12分
12分
考点:频率分布直方图;二项分布;应用意识


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015届广西桂林中学高二下学期期中考试理科数学试卷(解析版) 题型:选择题
函数f(x)=1+x- 在(0,2π)上是( )
在(0,2π)上是( )
A.增函数 B.在(0,π)上递增,在(π,2π)上递减
C.减函数 D.在(0,π)上递减,在(0,2π)上递增
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期第二次月考理科数学卷(解析版) 题型:选择题
用反证法证明命题“三角形的内角至少有一个不大于60?”时,应该先
A.假设三内角都不大于60?
B.假设三内角都大于60?
C.假设三内角至多有一个大于60?
D.假设三内角至多有两个大于60?
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期中段考文科数学试卷(解析版) 题型:选择题
独立性检验中,假设H0:变量X与变量Y没有关系,则在H0成立的情况下,P(K2≥6.635)≈0.010表示的意义是( )
A.在犯错误的概率不超过0.1%的前提下,认为“变量X与变量Y有关”
B.在犯错误的概率不超过0.1%的前提下,认为“变量X与变量Y无关”
C.有99%以上的把握认为“变量X与变量Y无关”
D.有99%以上的把握认为“变量X与变量Y有关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com