
分析 (1)若数列{an}为“6关联数列”,{an}前6项为等差数列,从第5项起为等比数列,可得a6=a1+5,a5=a1+4,且$\frac{{a}_{6}}{{a}_{5}}$=2,解得a1,即可求数列{an}的通项公式.
(2)由(1)得${S}_{n}=\left\{\begin{array}{l}{\frac{1}{2}{n}^{2}-\frac{7}{2}n,n≤4}\\{{2}^{n-4}-7,n≥5}\end{array}\right.$,可见数列{anSn}的最小项为a6S6=-6,即可证明:对任意n∈N*,anSn≥a6S6.
(3)由(1)知,当n≥6时,${a}_{n}={2}^{n-5}$,由此能求出${d}_{n}=\frac{{2}^{n-5}}{n+1}$.假设在数列{dn}中存在dm,dk,dp(其中m,k,p成等差数列),则(dk)2=dmdp,推导出k=m=p,这与题设矛盾.故在数列{dn}中不存在三项dm,dk,dp(其中m,k,p成等差数列)成等比数列.
解答 解:(1)∵数列{an}为“6关联数列”,
∴{an}前6项为等差数列,从第5项起为等比数列,
∴a6=a1+5,a5=a1+4,且$\frac{{a}_{6}}{{a}_{5}}$=$\frac{{a}_{1}+5}{{a}_{1}+4}$=2,解得a1=-3,
∴${a}_{n}=\left\{\begin{array}{l}{n-4,n≤4}\\{{2}^{n-5},n≥5}\end{array}\right.$.
(2)由(1)得${S}_{n}=\left\{\begin{array}{l}{\frac{1}{2}{n}^{2}-\frac{7}{2}n,n≤4}\\{{2}^{n-4}-7,n≥5}\end{array}\right.$,
{an}:-3,-2,-1,0,1,2,22,23,24,25,…,
{Sn}:-3,-5,-6,-6,-5,-3,1,9,25,…
{anSn}:9,10,6,0,-5,-6,4,72,400,…,
可见数列{anSn}的最小项为a6S6=-6,
证明:anSn=$\left\{\begin{array}{l}{\frac{1}{2}n(n-4)(n-7),n≤5}\\{{2}^{n-5}({2}^{n-4}-7),n≥6}\end{array}\right.$,
列举法知当n≤5时,(anSn)min=a5S5=-5;
当n≥6时,anSn=2•(2n-5)2-7•2n-5,n≥6,
设t=2n-5,则anSn=2t2-7t=2(t-$\frac{7}{4}$)2-7t=2(t-$\frac{7}{4}$)2-$\frac{49}{8}$≥2•22-7•2=-6.
(3)由(1)知,当n≥6时,${a}_{n}={2}^{n-5}$,
∵an+1=an+(n+2-1)dn,
2n-4=2n-5+(n+1)dn,∴${d}_{n}=\frac{{2}^{n-5}}{n+1}$.
假设在数列{dn}中存在dm,dk,dp(其中m,k,p成等差数列),
则(dk)2=dmdp,
∴($\frac{{2}^{k-5}}{k+1}$)2=$\frac{{2}^{m-5}}{m+1}•\frac{{2}^{p-5}}{p+1}$,$\frac{{2}^{2k-10}}{(k+1)^{2}}=\frac{{2}^{m+p-10}}{(m+1)(p+1)}$,(*)
∵m,p,k成等差数列,∴m+p=2k,(*)式可化简为(k+1)2=(m+1)(p+1),
即k2=mp,∴k=m=p,这与题设矛盾.
∴在数列{dn}中不存在三项dm,dk,dp(其中m,k,p成等差数列)成等比数列.
点评 本题考查数列的通项公式的求法,考查不等式的证明,考查满足条件的三项是否存在的判断与求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{10}{3}$ | C. | 2 | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+\sqrt{5}}{2}$ | B. | $\frac{1+\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{1+\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{1}{2}$x | B. | y=±2x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\sqrt{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
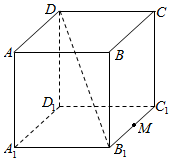 如图AC1是棱长为2的正方体,M为B1C1的中点,给出下列命题:
如图AC1是棱长为2的正方体,M为B1C1的中点,给出下列命题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com