
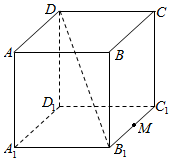
 如图AC1是棱长为2的正方体,M为B1C1的中点,给出下列命题:
如图AC1是棱长为2的正方体,M为B1C1的中点,给出下列命题:分析 ①根据异面直线所成的角进行求解.
②建立坐标系,利用四点共面建立方程关系进行求解,
③根据直线垂直确定P的运动轨迹,
④根据异面直线所成角的定义进行求解即可.
解答 证明:①连接AD1,B1D1,则AD1∥BC1,
则△AB1D1是正三角形,
则AD1与AB1所成的角即为AB1与BC1成的角,
即AB1与BC1成60°角;故①正确,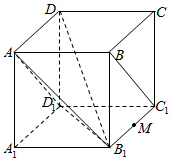
②若$\overrightarrow{CN}$=$\frac{1}{3}$$\overrightarrow{N{C}_{1}}$,面A1MN交CD于E,则CE=$\frac{1}{3}$;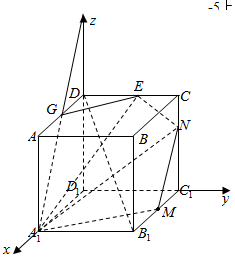
建立以D1为坐标原点,D1A1,D1C1,D1D分别为x,y,z轴的空间直角坐标系如图:
则A1(2,0,0),M(1,2,0),N(0,2,$\frac{3}{2}$),
设DE=t,则E(0,t,2),
∵A1,M,N,E四点共面,
∴存在实数x,y使$\overrightarrow{{A}_{1}E}$=x$\overrightarrow{{A}_{1}M}$+y$\overrightarrow{{A}_{1}N}$,
即(-2,t,2)=x(-1,2,0)+y(-2,2,$\frac{3}{2}$),
则$\left\{\begin{array}{l}{-x-2y=-2}\\{2x+2y=t}\\{\frac{3}{2}y=2}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-\frac{2}{3}}\\{y=\frac{4}{3}}\\{t=\frac{4}{3}}\end{array}\right.$,则DE=$\frac{4}{3}$,CE=2-$\frac{4}{3}$=$\frac{2}{3}$,
故②错误,
③取A1B1的中点H,BB1的中点K,
连接HM,HM,HK,
则DB1⊥HM,DB1⊥KM,
则DB1⊥平面HKM,
若MP⊥DB1,则M在平面HKM中,则M∈HK,
则HK=$\sqrt{2}$HB1=$\sqrt{2}$,即P点在正方形ABB1A1边界及内部运动,且MP⊥DB1,则P点轨迹长等于$\sqrt{2}$正确,故③正确;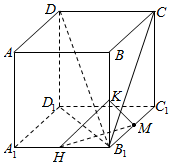
④建立如图的空间坐标系如图,
则A1(2,0,0),D(0,0,2),A(2,0,2),B1(2,2,0),
则$\overrightarrow{{D}_{1}A}$=(2,0,2),$\overrightarrow{D{A}_{1}}$=(2,0,-2),
∵E,F分别在DB1和A1C1上,且$\frac{DE}{E{B}_{1}}$=$\frac{{A}_{1}F}{F{C}_{1}}$=2,
∴$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{D{B}_{1}}$=$\frac{2}{3}$(2,2,-2)=($\frac{4}{3}$,$\frac{4}{3}$,-$\frac{4}{3}$),
则E($\frac{4}{3}$,$\frac{4}{3}$,$\frac{2}{3}$),
$\overrightarrow{{A}_{1}F}$=$\frac{2}{3}$$\overrightarrow{{A}_{1}{C}_{1}}$=$\frac{2}{3}$(-2,2,0)=(-$\frac{4}{3}$,$\frac{4}{3}$,0),
则F($\frac{2}{3}$,$\frac{4}{3}$,0),
则$\overrightarrow{EF}$=(-$\frac{2}{3}$,0,-$\frac{2}{3}$),
则cosα=|cos<$\overrightarrow{EF}$,$\overrightarrow{{D}_{1}A}$>|=|$\frac{-\frac{4}{3}-\frac{4}{3}}{\sqrt{4+4}•\sqrt{(-\frac{2}{3})^{2}+(-\frac{2}{3})^{2}}}$|=$\frac{\frac{8}{3}}{2\sqrt{2}•\frac{2\sqrt{2}}{3}}$=1,
则α=0
cosβ=|cos<$\overrightarrow{EF}$,$\overrightarrow{D{A}_{1}}$>|=|$\frac{-\frac{4}{3}+\frac{4}{3}}{\sqrt{4+4}•\sqrt{(-\frac{2}{3})^{2}+(-\frac{2}{3})^{2}}}$|=0,
则β=$\frac{π}{2}$,即α+β=$\frac{π}{2}$,故④正确,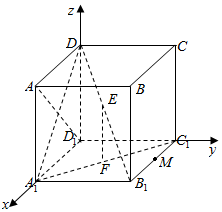
故答案为:①③④.
点评 本题主要考查命题的真假判断,涉及空间直线所成角,线面垂直的位置关系等,综合性较强,难度较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 0 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | A∪B=∅ | C. | A?B | D. | (∁UA)∩B={2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x(公顷) | 20 | 40 | 50 | 60 | 80 |
| y(℃) | 3 | 4 | 4 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com