
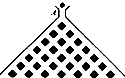
 如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是| 1 |
| 2 |
m-1 n-1 |
| 1 |
| 2 |
|
| C | 0 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| 1 |
| 16 |
| 5 |
| 16 |
| 5 |
| 8 |
| ξ | 3 | 2 | 1 | ||||||
| P |
|
|
|
| 1 |
| 16 |
| 5 |
| 6 |
| 5 |
| 8 |
| 23 |
| 16 |


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
| A、l个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,直三棱柱ABC-A1B1C1底面边长均为
如图,直三棱柱ABC-A1B1C1底面边长均为| 2 |
| A1D |
| A1C1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 居民区 | 低保户数 | 抽取低保户数 |
| A | 34 | 2 |
| B | 17 | x |
| C | 68 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 购地总费用 |
| 建筑面积 |
查看答案和解析>>
科目:高中数学 来源: 题型:
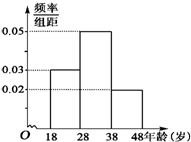 武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:
武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:| 组数 | 分组 | 回答正确的人数 | 占本组的频率 |
| 第1组 | [18,28) | 240 | x |
| 第2组 | [28,38) | 300 | 0.6 |
| 第3组 | [38,48] | a | 0.4 |
| t-40 |
查看答案和解析>>
科目:高中数学 来源: 题型:
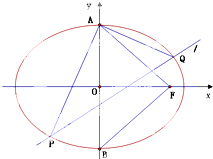 如图所示,A、B分别是椭圆C:
如图所示,A、B分别是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 认为作业多 | 认为作业不多 | 总数 | |
| 喜欢玩电脑游戏 | 20 | 10 | 30 |
| 不喜欢玩电脑游戏 | 5 | 15 | 20 |
| 总数 | 25 | 25 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com