
| 认为作业多 | 认为作业不多 | 总数 | |
| 喜欢玩电脑游戏 | 20 | 10 | 30 |
| 不喜欢玩电脑游戏 | 5 | 15 | 20 |
| 总数 | 25 | 25 | 50 |
| 25 |
| 50 |
| 1 |
| 2 |
| 20 |
| 50 |
| 2 |
| 5 |
| 5 |
| 25 |
| 4 |
| 10 |
| 2 |
| 5 |


科目:高中数学 来源: 题型:
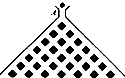 如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是| 1 |
| 2 |
m-1 n-1 |
| 1 |
| 2 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,用边长为60cm的正方形铁皮做一个无盖水箱,先在四角分别截去一个相同的小正方形,然后把四边翻折90°角,再焊接成无盖水箱,则水箱的最大容积为
如图所示,用边长为60cm的正方形铁皮做一个无盖水箱,先在四角分别截去一个相同的小正方形,然后把四边翻折90°角,再焊接成无盖水箱,则水箱的最大容积为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com