
【题目】已知三棱柱![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 与
与![]() 的中点,
的中点,![]() 为等边三角形,
为等边三角形,![]() ,
,![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)(i)求证:![]() 平面
平面![]() ;
;
(ii)求二面角![]() 的正弦值.
的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)(i)见解析(ii)![]()
【解析】
(Ⅰ)由![]() 推出
推出![]() 平面
平面![]() ,由
,由![]() 推出
推出![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]() ,由
,由![]() 平面PMN即可得证;(Ⅱ)(i)勾股定理证明
平面PMN即可得证;(Ⅱ)(i)勾股定理证明![]() 、
、![]() ,即可推出
,即可推出![]() 平面
平面![]() ;(ii)建立空间直角坐标系,求出平面AMN,平面BMN的法向量代入
;(ii)建立空间直角坐标系,求出平面AMN,平面BMN的法向量代入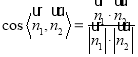 即可求得两向量夹角的余弦值,再求出正弦值即可.
即可求得两向量夹角的余弦值,再求出正弦值即可.
(Ⅰ)取![]() 中点
中点![]() ,连接MP,则
,连接MP,则![]() ,
,
因为![]() 平面ABC,
平面ABC,![]() 平面ABC,所以
平面ABC,所以![]() 平面
平面![]() ,
,
因为N、P分别![]() 的中点,所以
的中点,所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
因为![]() 平面ABC,
平面ABC,![]() 平面ABC,故
平面ABC,故![]() 平面
平面![]() ,
,
因为![]() ,
,![]() 平面PMN,
平面PMN,![]() 平面PMN,
平面PMN,
于是平面![]() 平面
平面![]() ,
,
又![]() 平面PMN,所以
平面PMN,所以![]() 平面
平面![]() .
.
(Ⅱ)(i)不妨设![]() ,则
,则![]() .
.
依题意![]() ,故
,故![]() 为等腰
为等腰![]() 底边上的中线,则
底边上的中线,则![]() .
.
于是![]() ,
,
因为![]() ,所以
,所以![]() ,同理
,同理![]() ,则
,则![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(ii)方法一:因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() 为等边三角形且
为等边三角形且![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,因为
,因为![]() 平面AMN,故平面
平面AMN,故平面![]() 平面
平面![]() .
.
设![]() ,则
,则![]() 为平面
为平面![]() 与平面
与平面![]() 的交线.过
的交线.过![]() 作
作![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() .又过
.又过![]() 作
作![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() ,
,![]() 即为二面角
即为二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() ,则
,则![]() ;
;
在![]() 中,
中,![]() .
.
所以![]() ,即二面角
,即二面角![]() 的正弦值是
的正弦值是![]() .
.
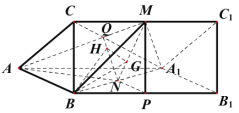
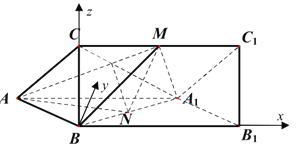
方法二:以![]() 为原点,建立如图所示的空间直角坐标系.则
为原点,建立如图所示的空间直角坐标系.则![]() ,
,![]() ,
, ,
,![]() ,
,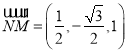 ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() .
.
由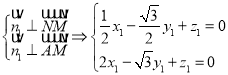 ,可取
,可取![]() ;
;
由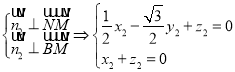 ,可取
,可取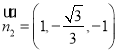 .
.
于是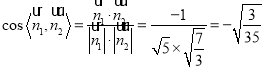 ,
,
所以二面角![]() 的正弦值是
的正弦值是![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程是![]() (t为参数),圆C的极坐标方程是ρ=4cos θ,求直线l被圆C截得的弦长.
(t为参数),圆C的极坐标方程是ρ=4cos θ,求直线l被圆C截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC—A1B1C1中,ACBC,D,E分别是A1B1,BC的中点.求证:

(1)平面ACD⊥平面BCC1B1;
(2)B1E∥平面ACD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】明代商人程大位在公元1592年编撰完成《算法统宗》一书.书中有如下问题:“今有女子善织,初日迟,次日加倍,第三日转速倍增,第四日又倍增,织成绢六丈七尺五寸.问各日织若干?”意思是:“有一位女子善于织布,第一天由于不熟悉有点慢,第二天起每天织的布都是前一天的2倍,已知她前四天共织布6丈7尺5寸,问这位女子每天织布多少?”根据文中的已知条件,可求得该女了第一天织布________尺,若织布一周(7天),共织________尺.(其中1丈为10尺,1尺为10寸)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数据的收集和整理在当今社会起到了举足轻重的作用,它用统计的方法来帮助人们分析以往的行为习惯,进而指导人们接下来的行动.
某支足球队的主教练打算从预备球员甲、乙两人中选一人为正式球员,他收集到了甲、乙两名球员近期5场比赛的传球成功次数,如下表:
场次 | 第一场 | 第二场 | 第三场 | 第四场 | 第五场 |
甲 | 28 | 33 | 36 | 38 | 45 |
乙 | 39 | 31 | 43 | 39 | 33 |
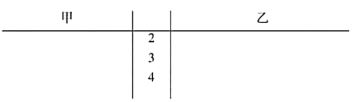
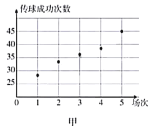
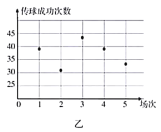
(1)根据这两名球员近期5场比赛的传球成功次数,完成茎叶图(茎表示十位,叶表示个位);分别在平面直角坐标系中画出两名球员的传球成功次数的散点图;
(2)求出甲、乙两名球员近期5场比赛的传球成功次数的平均值和方差;
(3)主教练根据球员每场比赛的传球成功次数分析出球员在场上的积极程度和技术水平,同时根据多场比赛的数据也可以分析出球员的状态和潜力.你认为主教练应选哪位球员?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中曲线C的参数方程为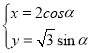 (
(![]() 为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线l过A,B两点,且这两点的极坐标分别为
为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线l过A,B两点,且这两点的极坐标分别为![]() .
.
(I)求C的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(II)若M为曲线C上一动点,求点M到直线l的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线C1的参数方程为![]() (t为参数,0<α<π),曲线C2的参数方程为
(t为参数,0<α<π),曲线C2的参数方程为 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C2的极坐标方程;
(2)设曲线C1与曲线C2的交点分别为A,B,M(﹣2,0),求|MA|2+|MB|2的最大值及此时直线C1的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com