
����Ŀ��ij�ҵ�ר��������A��B��C�������Ϳյ�����������������������ʾ��
��һ�� �ڶ��� ������ ������ ������
A������/̨ 12 8 15 22 18
B������/̨ 7 12 10 10 12
C������/̨ ![]()
![]()
![]()
![]()
![]()
��I����A�Ϳյ�ƽ��ÿ�ܵ�����������
����Ϊ���ٵ���յ���ʹ��������Ӹüҵ�ר����ڶ����۳���A��B�Ϳյ����ۼ�¼�У������ȡһ̨����鵽B�Ϳյ��ĸ��ʣ�
��III����֪C�Ϳյ���������������ƽ����Ϊ7������Ϊ4����ÿ����������![]() ������ͬ����C�Ϳյ��������е����������������ֻ��д�����ۣ�
������ͬ����C�Ϳյ��������е����������������ֻ��д�����ۣ�
���𰸡���I��15̨������![]() ������10̨
������10̨
��������
��I�������������ݣ����ƽ�����ļ��㹫ʽ��������������
�������衰�����ȡһ̨���鵽B�Ϳյ���Ϊ�¼�D�������������ݣ�ȷ���¼�D�����Ļ����¼��������Լ��ܵĻ����¼������������¼������ȼ�Ϊ������ʣ�
��III���ȸ������⣬��![]() �����ƽ�����뷽��õ�
�����ƽ�����뷽��õ�![]() �����
�����![]() ��Χ���ֱ�ȡ
��Χ���ֱ�ȡ![]() ��֤��ֱ���õ��������������Ϊֹ.
��֤��ֱ���õ��������������Ϊֹ.
��I��A�Ϳյ�ƽ��ÿ�ܵ���������![]() ��̨��
��̨��
�����衰�����ȡһ̨���鵽B�Ϳյ���Ϊ�¼�D��
���¼�D����12�������¼��������л����¼�����Ϊ![]() ������
������![]()
��������C�Ϳյ���ÿ����������![]() ������ͬ��
������ͬ��
���Բ�����![]() ����ΪC�Ϳյ���������������ƽ����Ϊ7������Ϊ4��
����ΪC�Ϳյ���������������ƽ����Ϊ7������Ϊ4��
����![]() ��
��
Ϊ����C�Ϳյ��������е�����������������ֻ����![]() ��ɣ�
��ɣ�
����![]() ��������֪
��������֪![]() ��
��
��![]() ʱ������
ʱ������![]()
����![]()
��ʱ��Ȼ��![]() ��������Ŀ����Ҫ���ÿ����������
��������Ŀ����Ҫ���ÿ����������![]() ������ͬì�ܣ���
������ͬì�ܣ���![]() .
.
��![]() ʱ������
ʱ������![]() ��
��
����![]() ����
����![]()
��������![]() ���������
���������![]() �����ֵΪ
�����ֵΪ![]() ��
��
���Ա���![]() ����
����![]() ��
��
����ʱ![]() ����֪
����֪![]() ���������⣬��C�Ϳյ��������е��������������Ϊ10̨.
���������⣬��C�Ϳյ��������е��������������Ϊ10̨.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}����a1+a2+a3+��an=2n��an��n��N+��������{bn}����bn= ![]() ����{bn}�е�������ֵ�� ��
����{bn}�е�������ֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABC��A1B1C1�У���֪����ABB1A1�����Σ�����BCC1B1�������Σ���A1�ڵ���ABC��ͶӰΪAB���е�D�� 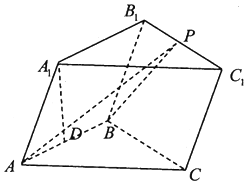
��1��֤����ƽ��AA1B1B��ƽ��BB1C1C��
��2����PΪB1C1��һ�㣬�� ![]() ��������A1��AB��P������ֵ��
��������A1��AB��P������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͳ�Ƽס�������ѧ����5��ѵ���ɼ�����λ���֣���������£�
ѧ�� | ��1�� | ��2�� | ��3�� | ��4�� | ��5�� |
�� | 65 | 80 | 70 | 85 | 75 |
�� | 80 | 70 | 75 | 80 | 70 |
��ɼ���Ϊ�ȶ��������С������λѧ���ɼ��ķ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������з���һ�ֲ�Ʒ���ò�Ʒÿ���ɱ�Ϊ5Ԫ�����ò�Ʒ�������ⶨ�ļ۸�������ۣ��õ��������ݣ�
���� | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
���� | 90 | 84 | 83 | 80 | 75 | 68 |
��1��������![]() ���������ڵ���
���������ڵ���![]() ��Ԫ�������Իع鷽��
��Ԫ�������Իع鷽��![]() ��
��
��2�������۶�Ϊ10Ԫ����������Ϊ���ټ���
��3����������![]() ���ڵ���
���ڵ���![]() �����Իع鷽�̣�Ҫʹ����
�����Իع鷽�̣�Ҫʹ����![]() ���Ӧ���۸�Ϊ���٣�
���Ӧ���۸�Ϊ���٣�
�ο���ʽ�� ��
��![]() .�ο����ݣ�
.�ο����ݣ�![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij��˾Ϊ֣��������ij������Ʒ���ù�˾��̶��ɱ�Ϊ10��Ԫ��ÿ����ǧ������Ͷ��2 .7��Ԫ����ù�˾���ڹ�������������Ʒ��xǧ����ȫ��������;ÿǧ������������ΪR(x)��Ԫ��
�� ��
��
(I)д��������W(��Ԫ�����ڸ�������Ʒx(ǧ�����ĺ�������ʽ��
��II�������Ϊ����ǧ��ʱ���ù�˾�ڸ�������Ʒ���������������������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}�Ĺ���d��Ϊ0���� ![]() ��
�� ![]() ������
������ ![]() ������k1��k2������kn�������ɵȱ����У�����Ϊq��
������k1��k2������kn�������ɵȱ����У�����Ϊq��
��1����k1=1��k2=3��k3=8���� ![]() ��ֵ��
��ֵ��
��2���� ![]() Ϊ��ֵʱ������{kn}Ϊ�ȱ����У�
Ϊ��ֵʱ������{kn}Ϊ�ȱ����У�
��3��������{kn}Ϊ�ȱ����У��Ҷ�������n��N* �� ����ʽ ![]() ���������a1��ȡֵ��Χ��
���������a1��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�������f��x����[a��b]�ϴ���x1 �� x2��a��x1��x2��b������ ![]() ��
�� ![]() ��ƺ���f��x����[a��b]�ϵġ���ֵ����������֪����
��ƺ���f��x����[a��b]�ϵġ���ֵ����������֪���� ![]() ��[0��m]�ϵġ���ֵ����������ʵ��m��ȡֵ��Χ�ǣ� ��
��[0��m]�ϵġ���ֵ����������ʵ��m��ȡֵ��Χ�ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() :
: ![]() ����
����![]() ��ֱ�߽�������
��ֱ�߽�������![]() ��
��![]() ���㣬��
���㣬��![]()
(1)���� ![]() ����
����![]() ��ĶԳƵ�Ϊ
��ĶԳƵ�Ϊ![]() ����֤��ֱ��
����֤��ֱ��![]() ����������
����������![]() �Ľ���
�Ľ���![]() ��
��
(2)��![]() ��
��![]() ���ʱ��ֱ��
���ʱ��ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com