
 青岛市为办好“世园会”,征集了1000名志愿者,现对他们的年龄抽样统计后,得到如图所示的频率分布直方图,年龄在[25,30]内的数据不慎丢失,依旧此图可得
青岛市为办好“世园会”,征集了1000名志愿者,现对他们的年龄抽样统计后,得到如图所示的频率分布直方图,年龄在[25,30]内的数据不慎丢失,依旧此图可得分析 通过对频率分布直方图的读取,可推知出[25,30)段所占的比例,继而求出该段的高度.算出[25,35)段所占的比例,求出该段人数.
解答 解:(1)除[25,30)段的比例,其它各段的比例和为:(0.01+0.07+0.06+0.02)×5=0.8.所以[25,30)段所占的比例为1-0.8=0.2
所以该段对应的小长方形的面积为0.2.所以高度为$\frac{0.2}{5}=0.04$.
(2)年龄在[25,35)内的比例为(0.04+0.07)×5=0.55
所以1000名志愿者中年龄在[25,35)内的人数为1000×0.55=550人
故答案为:0.04,550
点评 本题主要考查频率分布直方图的读图能力,属于简单题型,注意纵坐标意义.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
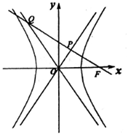 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2.
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -$\frac{2}{5}$ | C. | -$\frac{3}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com