
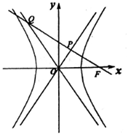
 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2.
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2. 分析 通过联立渐近线y=$\frac{b}{a}$x与直线PF的方程,可得P($\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),利用中点坐标公式可得Q(2$\frac{{a}^{2}}{c}$-c,2$\frac{ab}{c}$),将点Q代入渐近线y=-$\frac{b}{a}$x,计算即得结论.
解答 解:设F(c,0),相应的渐近线:y=$\frac{b}{a}$x,
则直线PF的斜率为-$\frac{a}{b}$,其方程为:y=-$\frac{a}{b}$(x-c),
设P(t,$\frac{b}{a}$t),代入直线PF的方程,
得:$\frac{b}{a}$t=-$\frac{a}{b}$(t-c),解得:t=$\frac{{a}^{2}}{c}$,即P($\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),
∵|PF|=|PQ|,即点P为线段FQ的中点,
∴Q(2$\frac{{a}^{2}}{c}$-c,2$\frac{ab}{c}$),
∵点Q在渐近线y=-$\frac{b}{a}$x上,
∴2$\frac{ab}{c}$=-$\frac{b}{a}$(2$\frac{{a}^{2}}{c}$-c),
化简得:$\frac{c}{a}$=2,即离心率为2,
故答案为:2.
点评 本题主要考查双曲线的几何性质,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | a<c<b | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 将正方形ABCD分割成n2(n≥2,n∈N)个全等的小正方形(图1,图2分别给出了n=2,3的情形),在每个小正方形的顶点各放置一个数,使位于正方形ABCD的四边及平行于某边的任一直线上的数都分别依次成等差数列,若顶点A,B,C,D处的四个数互不相同且和为1,记所有顶点上的数之和为f(n),则f(4)=( )
将正方形ABCD分割成n2(n≥2,n∈N)个全等的小正方形(图1,图2分别给出了n=2,3的情形),在每个小正方形的顶点各放置一个数,使位于正方形ABCD的四边及平行于某边的任一直线上的数都分别依次成等差数列,若顶点A,B,C,D处的四个数互不相同且和为1,记所有顶点上的数之和为f(n),则f(4)=( )| A. | 4 | B. | B6 | C. | $\frac{25}{4}$ | D. | $\frac{13}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计),易拉罐的体积为108πml.设圆柱的高度为hcm,底面半径半径为rcm,且h≥4r,假设该易拉罐的制造费用仅与其表面积有关,已知易拉罐侧面制造费用为m元/cm2,易拉罐上下底面的制造费用均为n元/cm2(m,n为常数)
某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计),易拉罐的体积为108πml.设圆柱的高度为hcm,底面半径半径为rcm,且h≥4r,假设该易拉罐的制造费用仅与其表面积有关,已知易拉罐侧面制造费用为m元/cm2,易拉罐上下底面的制造费用均为n元/cm2(m,n为常数)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,+∞) | B. | (1,3) | C. | (-∞,3) | D. | (-∞,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 青岛市为办好“世园会”,征集了1000名志愿者,现对他们的年龄抽样统计后,得到如图所示的频率分布直方图,年龄在[25,30]内的数据不慎丢失,依旧此图可得
青岛市为办好“世园会”,征集了1000名志愿者,现对他们的年龄抽样统计后,得到如图所示的频率分布直方图,年龄在[25,30]内的数据不慎丢失,依旧此图可得查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10. 828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com