
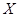 ,求
,求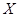 的分布列和数学期望.
的分布列和数学期望.科目:高中数学 来源:不详 题型:解答题
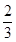 ,被乙小组攻克的概率为
,被乙小组攻克的概率为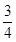 ,
,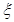 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求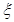 的分布列及数学期望
的分布列及数学期望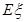 ;
;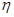 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数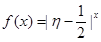 在定义域内单调递增”为事件C,求事件C发生的概率;
在定义域内单调递增”为事件C,求事件C发生的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中任选出两位同学,共同帮助成绩在
中任选出两位同学,共同帮助成绩在 中的某一个同学,试列出所有基本事件;若
中的某一个同学,试列出所有基本事件;若 同学成绩为43分,
同学成绩为43分, 同学成绩为95分,求
同学成绩为95分,求 、
、 两同学恰好被安排在“二帮一”中同一小组的概率.
两同学恰好被安排在“二帮一”中同一小组的概率.| 分 组 | 频 数 | 频 率 |
| [40, 50 ) | 2 | 0.04 |
| [ 50, 60 ) | 3 | 0.06 |
| [ 60, 70 ) | 14 | 0.28 |
| [ 70, 80 ) | 15 | 0.30 |
| [ 80, 90 ) | | |
| [ 90, 100 ] | 4 | 0.08 |
| 合 计 | | |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 0.785,汽车的碳排放量(千克)=油耗公升数
0.785,汽车的碳排放量(千克)=油耗公升数 0.785等。怀化某中学高一一同学利用寒假在两个小区逐户进行了一次生活习惯是否符合低碳观念的调查。若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”。这二族人数占各自小区总人数的比例P数据如右:
0.785等。怀化某中学高一一同学利用寒假在两个小区逐户进行了一次生活习惯是否符合低碳观念的调查。若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”。这二族人数占各自小区总人数的比例P数据如右:
 表示25个人中低碳族人数,求E
表示25个人中低碳族人数,求E .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com