
已知二次函数 (其中
(其中 )满足下列3个条件:
)满足下列3个条件:
① 的图象过坐标原点;
的图象过坐标原点;
②对于任意 都有
都有 成立;
成立;
③方程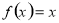 有两个相等的实数根,令
有两个相等的实数根,令 (其中
(其中 ),
),
(1)求函数 的表达式;
的表达式;
(2)求函数 的单调区间(直接写出结果即可);
的单调区间(直接写出结果即可);
(3)研究函数 在区间
在区间 上的零点个数.
上的零点个数.
(1)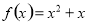 ;(2)当
;(2)当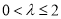 时,函数
时,函数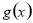 增区间为
增区间为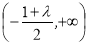 ,减区间为
,减区间为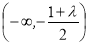 ;
;
当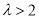 时,函数
时,函数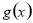 的增区间为
的增区间为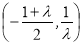 、
、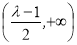 ,减区间为
,减区间为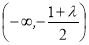 、
、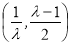 .;(3)当
.;(3)当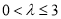 时,函数
时,函数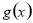 在区间
在区间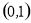 上只有一个零点;当
上只有一个零点;当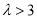 时,函数
时,函数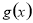 在区间
在区间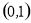 上有两个不同的零点.
上有两个不同的零点.
【解析】
试题分析:(1)通过已知给的三个条件逐一求出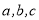 的值,对于①可以求出
的值,对于①可以求出 ,对于②可以得知函数的对称轴为
,对于②可以得知函数的对称轴为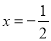 ,可以求出
,可以求出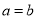 ,对于③可以根据判别式等于
,对于③可以根据判别式等于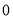 ,求得
,求得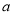 的值,则函数表达式就得出.(2)由于函数
的值,则函数表达式就得出.(2)由于函数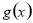 是带有参数和绝对值的函数,所以需要讨论,首先需要讨论去掉绝对值符号,会得知函数
是带有参数和绝对值的函数,所以需要讨论,首先需要讨论去掉绝对值符号,会得知函数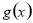 为分段函数,而每段区间又恰好为二次函数,再讨论二次函数对称轴在每段区间的位置关系,就可以得到
为分段函数,而每段区间又恰好为二次函数,再讨论二次函数对称轴在每段区间的位置关系,就可以得到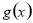 的单调区间.(3)由于第(2)问得知
的单调区间.(3)由于第(2)问得知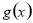 的单调区间,只需要讨论
的单调区间,只需要讨论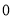 ,
, 和单调区间端点的位置关系以及正负情况,再通过函数的零点的存在性定理,就可以得出结论.
和单调区间端点的位置关系以及正负情况,再通过函数的零点的存在性定理,就可以得出结论.
试题解析:(1)由题意得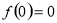 ,即
,即 . 1分
. 1分
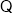 对于任意
对于任意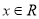 都有
都有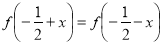 成立,
成立,
 函数
函数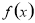 的对称轴为
的对称轴为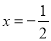 ,即
,即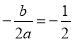 ,即
,即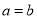 .
.

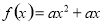 ,
,
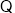 方程
方程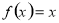 仅有一根,即方程
仅有一根,即方程 仅有一根,
仅有一根,

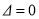 ,即
,即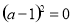 ,即
,即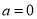 .
.

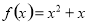 . 4分
. 4分
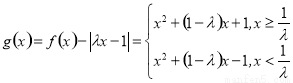 .
.
①当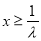 时,函数
时,函数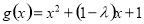 的对称轴为
的对称轴为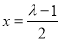 ,
,
若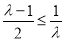 ,即
,即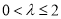 ,函数
,函数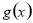 在
在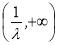 上单调递增;
上单调递增;
若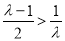 ,即
,即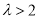 ,函数
,函数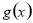 在
在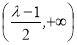 上单调递增,在
上单调递增,在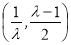 上单调递减.
上单调递减.
②当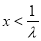 时,函数
时,函数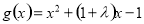 的对称轴为
的对称轴为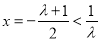 ,
,
则函数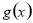 在
在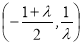 上单调递增,在
上单调递增,在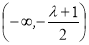 上单调递减.
上单调递减.
综上所述:
当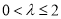 时,函数
时,函数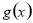 增区间为
增区间为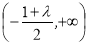 ,减区间为
,减区间为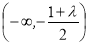 ;
;
当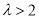 时,函数
时,函数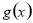 的增区间为
的增区间为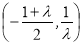 、
、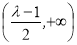 ,减区间为
,减区间为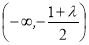 、
、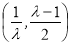 9分
9分
①当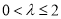 时,由(2)知函数
时,由(2)知函数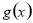 在区间
在区间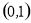 上单调递增,
上单调递增,
又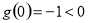 ,
,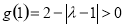 ,
,
故函数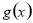 在区间
在区间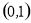 上只有一个零点. 12分
上只有一个零点. 12分
②当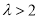 时,则
时,则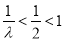 ,而
,而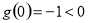 ,
,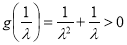 ,
,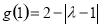 ,
,
(ⅰ)若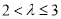 ,由于
,由于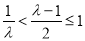 ,
,
且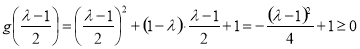 ,
,
此时,函数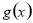 在区间
在区间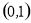 上只有一个零点;
上只有一个零点;
(ⅱ)若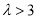 ,由于
,由于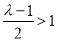 且
且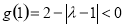 ,此时
,此时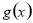 在区间
在区间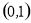 上有两个不同的零点.
上有两个不同的零点.
综上所述:
当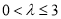 时,函数
时,函数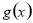 在区间
在区间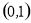 上只有一个零点;
上只有一个零点;
当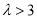 时,函数
时,函数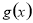 在区间
在区间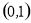 上有两个不同的零点. 16分
上有两个不同的零点. 16分
考点:1、求二次函数表达式.2、求解带有参数和绝对值符号的函数的单调性.3、函数零点的存在性定理.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:2014-2015学年江苏淮安涟水中学高二上学期第一次模块检测数学试卷(解析版) 题型:填空题
如图所示,已知一个多面体的平面展开图由一个边长为2的正方形和4个边长为2的正三角形组成,则该多面体的体积是________.

查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省高二10月月考数学试卷(解析版) 题型:选择题
已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公
差为( )
A. 5 B.4 C. 3 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com