Question

15．已知函数f（x）=|x-2|，g（x）=-|x+3|+m．
（1）解关于x的不等式f（x）-$\frac{1}{4}$x-1＞0；
（2）若函数f（x）的图象恒在函数g（x）图象的上方，求m的取值范围．

Answer 1

分析 （1）关于x的不等式f（x）-$\frac{1}{4}$x-1＞0，即|x-2|＞$\frac{x}{4}$+1，即x-2＞$\frac{x}{4}$+1 或x-2＜-（ $\frac{x}{4}$+1 ），由此求得它的解集．
（2）若函数f（x）的图象恒在函数g（x）图象的上方，画出图形，数形结合求得m的范围．

解答 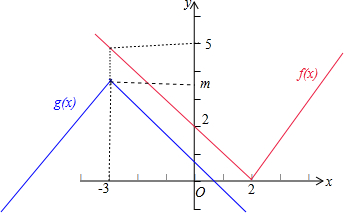解：（1）关于x的不等式f（x）-$\frac{1}{4}$x-1＞0，即|x-2|＞$\frac{x}{4}$+1，
∴x-2＞$\frac{x}{4}$+1 或x-2＜-（ $\frac{x}{4}$+1 ）．
求得 x＞4或 x＜$\frac{4}{5}$，故不等式的解集为{x|x＞4或 x＜$\frac{4}{5}$ }．
（2）若函数f（x）的图象恒在函数g（x）图象的上方，如图所示：
故有m＜5．

点评 本题主要考查绝对值不等式的解法，函数的恒成立问题，体现了数形结合的数学思想，属于基础题．