③
分析:对于①利用周期的定义判断正误;
对于②利用三角函数图象的平移即可判断正误;
对于③求出函数的对称中心,判断正误即可;
对于④求出函数的最小值即可判断正误.
解答:①函数y=4cos2x,x∈[-l0π,10π]不是周期函数,不满足周期的定义,所以不正确;
②函数y=4cos2x的图象,可由y=4sin2x的图象向右平移

个单位,得到函数y=4sin2(x-

)=-4cos2x的图象,所以不正确;
③函数y=4cos(2x+θ)的图象关于点(

,0)对称,所以2×

+θ=kπ+

,k∈Z,即θ=kπ+

(k∈Z);所以函数y=4cos(2x+θ)的图象关于点(

,0)对称的-个必要不充分条件是θ=

π+

(k∈Z),正确;
④函数y=
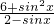
表示点(2,6)与(sinx,-sin
2x)连线的斜率的范围,求出过(2,6)与y=-x
2切线的斜率,
设过(2,6)的直线为y-6=k(x-2),联立方程组可得x
2+kx-2k+6=0,相切所以△=0,解得k=2

-4,
此时x=
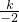
=2-

∉[-1,1],∴函数的最小值为2

-4.不正确.
故答案为:③.
点评:本题是中档题,考查三角函数的基本知识,周期、对称中心图形的平移,函数的最值,注意函数的最值的求法利用直线的斜率,曲线的参数方程的应用,考查计算能力.

 个单位得到;
个单位得到; ,0)对称的-个必要不充分条件是θ=
,0)对称的-个必要不充分条件是θ= π+
π+ (k∈Z);
(k∈Z);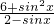 的最小值为2
的最小值为2 -4.
-4. 个单位,得到函数y=4sin2(x-
个单位,得到函数y=4sin2(x- )=-4cos2x的图象,所以不正确;
)=-4cos2x的图象,所以不正确; ,0)对称,所以2×
,0)对称,所以2× +θ=kπ+
+θ=kπ+ ,k∈Z,即θ=kπ+
,k∈Z,即θ=kπ+ (k∈Z);所以函数y=4cos(2x+θ)的图象关于点(
(k∈Z);所以函数y=4cos(2x+θ)的图象关于点( ,0)对称的-个必要不充分条件是θ=
,0)对称的-个必要不充分条件是θ= π+
π+ (k∈Z),正确;
(k∈Z),正确;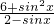 表示点(2,6)与(sinx,-sin2x)连线的斜率的范围,求出过(2,6)与y=-x2切线的斜率,
表示点(2,6)与(sinx,-sin2x)连线的斜率的范围,求出过(2,6)与y=-x2切线的斜率, -4,
-4,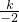 =2-
=2- ∉[-1,1],∴函数的最小值为2
∉[-1,1],∴函数的最小值为2 -4.不正确.
-4.不正确.

 发散思维新课堂系列答案
发散思维新课堂系列答案