
已知多面体ABCDFE中, 四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD, O、M分别为AB、FC的中点,且AB = 2,AD = EF = 1.

(1)求证:AF⊥平面FBC;
(2)求证:OM∥平面DAF;
(3)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD∶VF-CBE 的值.
(1)(2)见解析(3)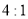
【解析】
试题分析:(1)要证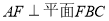 ,则需要证明
,则需要证明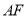 与平面
与平面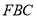 内的两条相交直线垂直,而根据题意已知
内的两条相交直线垂直,而根据题意已知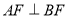 ,故只需再根据题意平面
,故只需再根据题意平面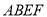 ⊥平面
⊥平面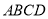 ,可证
,可证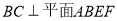 ,从而证明
,从而证明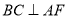 ,则可证明结论.
,则可证明结论.
(2)要证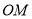 ∥平面
∥平面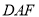 ,则需要在平面
,则需要在平面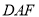 内找一条直线与
内找一条直线与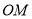 平行,根据点
平行,根据点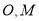 都是中点的特点, 取
都是中点的特点, 取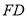 中点
中点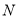 ,证明四边形
,证明四边形 为平行四边形,即有
为平行四边形,即有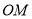 ∥
∥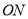 ,则可证明结论.
,则可证明结论.
(3)要求体积比,首先得找到体积,根据题意可知,分割后形成了两个棱锥,一个四棱锥,一个三棱锥;根据棱锥的体积公式,得找到底面积和高,而其中四棱锥的底面和高比较容易确定,而三棱锥中关键是确定底面和高,确定的依据就是是否有现成的线面垂直,显然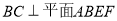 ,所以确定底面为
,所以确定底面为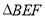 高
高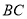 .最后分别求体积做比值即可.
.最后分别求体积做比值即可.
试题解析:(1)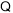 平面
平面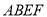 ⊥平面
⊥平面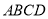 ,平面
,平面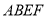
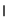 平面
平面 ,
,
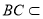 平面
平面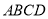 ,而四边形
,而四边形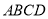 为矩形
为矩形 ,
,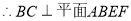
.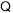
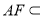 平面
平面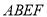
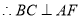
则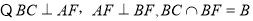 ,
,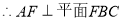
(2)取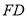 中点
中点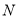 ,连接
,连接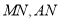 ,则
,则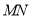 ∥
∥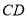 ,且
,且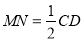 ,又四边形
,又四边形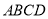 为矩形,
为矩形,
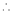
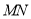 ∥
∥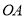 ,且
,且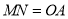
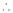 四边形
四边形 为平行四边形,
为平行四边形,
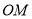 ∥
∥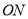
又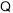
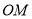
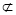 平面
平面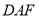 ,
,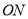
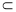 平面
平面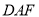
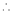
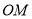 ∥平面
∥平面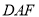
(3)过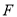 作
作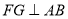 于
于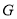 ,由题意可得:
,由题意可得: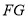
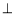 平面
平面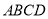 .
.
所以: .
.
因为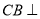 平面
平面 , 所以
, 所以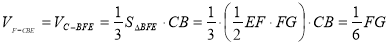
所以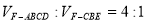
考点:面面垂直,线面垂直,线线垂直;线面平行的判定;棱锥体积转化及计算.


科目:高中数学 来源:2016届广东省梅州市高一上学期质检数学试卷(解析版) 题型:选择题
sin 34°sin 26°-cos 34°cos 26°的值是 ( )
A. B.
B.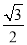 C.-
C.- D.-
D.-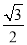
查看答案和解析>>
科目:高中数学 来源:2016届广东省高一下学期第一次阶段考试数学试卷(解析版) 题型:选择题
设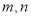 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,给出下列条件,能得到
是两个不同的平面,给出下列条件,能得到 的是( )
的是( )
A.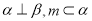 B.
B. C.
C.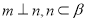 D.
D.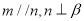
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com