
已知函数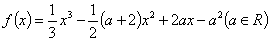 。
。
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若a=4,y=f(x)的图像与直线y=m有三个交点,求m的取值范围。
已知函数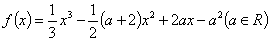 。
。
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若a=4,y=f(x)的图像与直线y=m有三个交点,求m的取值范围。
解:(Ⅰ)函数 的定义域为
的定义域为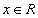 ,
,

①当a=2时, 恒成立,
恒成立, 在R上是增函数。
在R上是增函数。
②当a<2时,f'(x)≥0在(-∞,a]和[2,+∞)上恒成立,f'(x)≤0在
[a,2]上恒成立.
∴a<2时f(x)的增区间为(-∞,a]和[2,+∞),f(x)的减区间为[a,2].
③当a>2时,f'(x)≥0在(-∞,2]和[a,+∞)上恒成立,f'(x)≤0在
[2,a]上恒成立,
∴a>2时,f(x)的增区间为(-∞,2]和[a,+∞),f(x)的减区间为[2,a].
(Ⅱ)若a=4,由(Ⅰ)可得f(x)在(-∞,2]上单调递增,在[4,+∞)上单调递增,在[2,4]上单调递减。——————10分
f(x)极小值=f(4)= , ----11分 f(2)极大值=f(2)=
, ----11分 f(2)极大值=f(2)= ,
,
∴y=f(x)的图像与直线y=m有三个交点时m的取值范围是( ,
, )。
)。


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
男运动员6名,女运动员4名,其中男女队长各1人,从中
选5人外出比赛,下列情形各有多少种选派方法
⑴男3名,女2名 ⑵队长至少有1人参加
⑶至少1名女运动员 ⑷既要有队长,又要有女运动员
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)是定义在正整数集上的函数,且f(x)满足:“当f(k)≥k2成立时,总可推出f(k+1)≥(k+1)2成立”.那么,下列命题总成立的是( )
A.若f(1)<1成立,则f(10)<100成立
B.若f(2)<4成立,则f(1)≥1成立
C.若f(3)≥9成立,则当k≥1时,均有f(k)≥k2成立
D.若f(4)≥16成立,则当k≥4时,均有f(k)≥k2成立
查看答案和解析>>
科目:高中数学 来源: 题型:
在长为12 cm的线段AB上任取一点C.现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积小于32 cm2的概率为…………………………… ( )
A.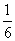 B.
B.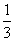 C.
C.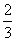 D.
D.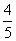
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com