
【题目】已知实数a、b满足:a>0,b>0.
(1)若x∈R,求证:|x+a|+|x﹣b|≥2 ![]() .
.
(2)若a+b=1,求证: ![]() +
+ ![]() +
+ ![]() ≥12.
≥12.
【答案】
(1)证明:由a>0,b>0,可得
|x+a|+|x﹣b|≥|(x+a)﹣(x﹣b)|=a+b≥2 ![]() ,
,
当且仅当a=b取得等号
(2)证明:由a,b>0,1=a+b≥2 ![]() ,
,
可得ab≤ ![]() ,即
,即 ![]() ≥4,
≥4,
则 ![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() ≥12,
≥12,
当且仅当a=b= ![]() ,取得等号
,取得等号
【解析】(1)运用绝对值不等式的性质和均值不等式,即可得证;(2)由均值不等式可得ab≤ ![]() ,即
,即 ![]() ≥4,原不等式左边化简即为
≥4,原不等式左边化简即为 ![]() ,即可得证.
,即可得证.
【考点精析】解答此题的关键在于理解不等式的证明的相关知识,掌握不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】小王每天自己开车上班,他在路上所用的时间![]() (分钟)与道路的拥堵情况有关.小王在一年中随机记录了200次上班在路上所用的时间,其频数统计如下表,用频率近似代替概率.
(分钟)与道路的拥堵情况有关.小王在一年中随机记录了200次上班在路上所用的时间,其频数统计如下表,用频率近似代替概率.
| 15 | 20 | 25 | 30 |
频数(次) | 50 | 50 | 60 | 40 |
(Ⅰ)求小王上班在路上所用时间的数学期望![]() ;
;
(Ⅱ)若小王一周上班5天,每天的道路拥堵情况彼此独立,设一周内上班在路上所用时间不超过![]() 的天数为
的天数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(x0 , 0),B(0,y0)两点分别在x轴和y轴上运动,且|AB|=1,若动点P(x,y)满足 ![]() .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线l1与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程;
(3)直线l2:x=ty+1与曲线C交于A、B两点,E(1,0),试问:当t变化时,是否存在一直线l2 , 使△ABE的面积为 ![]() ?若存在,求出直线l2的方程;若不存在,说明理由.
?若存在,求出直线l2的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公比小于1的等比数列{an}的前n项和为Sn , a1= ![]() ,且13a2=3S3(n∈N*).
,且13a2=3S3(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log3(1﹣Sn+1),若 ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() ,求n.
,求n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个定点![]() ,动点
,动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 与曲线
与曲线![]() 交于不同的
交于不同的![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率;
的斜率;
(3)若![]() ,
, ![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点.
是否过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左焦点为F,离心率为
=1(a>0,b>0)的左焦点为F,离心率为 ![]() .若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
.若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
A.![]()
=1
B.![]()
=1
C.![]()
=1
D.![]()
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C与A,B两点,圆M是以线段AB为直径的圆.
(Ⅰ)证明:坐标原点O在圆M上;
(Ⅱ)设圆M过点P(4,﹣2),求直线l与圆M的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在同一个平面内,向量 ![]() ,
, ![]() ,
, ![]() 的模分别为1,1,
的模分别为1,1, ![]() ,
, ![]() 与
与 ![]() 的夹角为α,且tanα=7,
的夹角为α,且tanα=7, ![]() 与
与 ![]() 的夹角为45°.若
的夹角为45°.若 ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),则m+n= .
(m,n∈R),则m+n= . 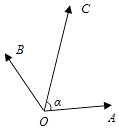
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com