
分析 利用抛物线的定义和|AF|=|AB|+1就可得出|AB|=xA,同理可得:|CD|=xD,要分l⊥x轴和l不垂直x轴两种情况分别求值,当l⊥x轴时易求,当l不垂直x轴时,将直线的方程代入抛物线方程,利用根与系数关系可求得.
解答  解:∵y2=4x,焦点F(1,0),准线 l0:x=-1.
解:∵y2=4x,焦点F(1,0),准线 l0:x=-1.
由定义得:|AF|=xA+1,
又∵|AF|=|AB|+1,∴|AB|=xA,
同理:|CD|=xD,
当l⊥x轴时,则xD=xA=1,∴|AB|•|CD|=1
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,
∴xAxD=1,∴|AB|•|CD|=1
综上所述,|AB|•|CD|=1,
故答案为1.
点评 本题主要考查抛物线的定义、一元二次方程的根与系数关系,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
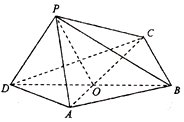 如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,BD=2$\sqrt{3}$,AC与BD交于O点.将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为θ,且P点在平面ABCD内的射影落在△ACD内.
如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,BD=2$\sqrt{3}$,AC与BD交于O点.将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为θ,且P点在平面ABCD内的射影落在△ACD内.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1-$\sqrt{2}$) | B. | ($\sqrt{2}$,+∞) | C. | (1,2$\sqrt{2}$) | D. | (2$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>1 | B. | $m>\frac{1}{2}$ | C. | m>2 | D. | m≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20% | B. | 25% | C. | 40% | D. | 80% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com