Question

10．设双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点为F₁，左顶点为A，过F₁作x轴的垂线交双曲线于P、Q两点，过P作PM垂直QA于M，过Q作QN垂直PA于N，设PM与QN的交点为B，若B到直线PQ的距离大于a+$\sqrt{{a}^{2}+{b}^{2}}$，则该双曲线的离心率取值范围是（　　）

• A． （1-$\sqrt{2}$）
• B． （$\sqrt{2}$，+∞）
• C． （1，2$\sqrt{2}$）
• D． （2$\sqrt{2}$，+∞）

Answer 1

分析 根据双曲线的对称性，则B（x，0），由k_BP•k_AQ=-1，求得c+x=-$\frac{{b}^{4}}{{a}^{2}（a-c）}$，由B到直线PQ的距离d=x+c，由丨-$\frac{{b}^{4}}{{a}^{2}（a-c）}$丨＞a+$\sqrt{{a}^{2}+{b}^{2}}$，即可求得$\frac{b}{a}$＞1，利用双曲线的离心率公式即可求得e的取值范围．

解答 解：由题意可知：A（-a，0），P（-c，$\frac{{b}^{2}}{a}$），Q（-c，-$\frac{{b}^{2}}{a}$），
由双曲线的对称性可知B在x轴上，设B（x，0），
则BP⊥AQ，
则k_BP•k_AQ=-1，
∴$\frac{-\frac{{b}^{2}}{a}}{-c-x}$•$\frac{\frac{{b}^{2}}{a}}{-c+a}$=-1，
则c+x=-$\frac{{b}^{4}}{{a}^{2}（a-c）}$，
由B到直线PQ的距离d=x+c，
∴丨-$\frac{{b}^{4}}{{a}^{2}（a-c）}$丨＞a+$\sqrt{{a}^{2}+{b}^{2}}$，则$\frac{{b}^{4}}{{a}^{2}}$＞c²-a²=b²，
∴$\frac{b}{a}$＞1，
由椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$＞$\sqrt{2}$，
双曲线的离心率取值范围（$\sqrt{2}$，+∞），
故选B．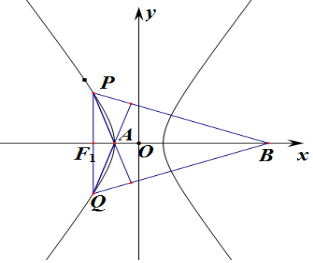

点评 本题考查双曲线的简单几何性质，考查双曲线通径的求法，直线的斜率公式，考查计算能力，属于中档题．