
分析 根据等差和等比的类比时,主要是“和”与“积”之间的类比,在等差中为和在等比中为积,按此规律即可得到结论.
解答 解:根据等比性质可知$\root{21}{{a}_{1993}•{a}_{1994}•{a}_{1995}…{a}_{2013}}$=$\root{4005}{{a}_{1}•{a}_{2}•{a}_{3}…{a}_{4005}}$=a2003,
所以根据等差数列中,有$\frac{{b}_{1993}+{b}_{1994}+…+{b}_{2013}}{21}$=$\frac{{b}_{1}+{b}_{2}+…+{b}_{4005}}{4005}$.
故答案为$\frac{{b}_{1993}+{b}_{1994}+…+{b}_{2013}}{21}$=$\frac{{b}_{1}+{b}_{2}+…+{b}_{4005}}{4005}$.
点评 类比推理是指根据两个(或两类)对象之间具有(或不具有)某些相同或相似的性质,而且已知其中一个(或另一类)还具有(或不具有)另一性质,由此推出另一个(或另一类)对象也具有(或不具有)这一性质.


科目:高中数学 来源: 题型:解答题
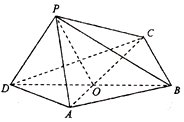 如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,BD=2$\sqrt{3}$,AC与BD交于O点.将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为θ,且P点在平面ABCD内的射影落在△ACD内.
如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,BD=2$\sqrt{3}$,AC与BD交于O点.将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为θ,且P点在平面ABCD内的射影落在△ACD内.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{18}{35}$ | B. | $\frac{15}{35}$ | C. | $\frac{12}{35}$ | D. | $\frac{9}{35}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1-$\sqrt{2}$) | B. | ($\sqrt{2}$,+∞) | C. | (1,2$\sqrt{2}$) | D. | (2$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20% | B. | 25% | C. | 40% | D. | 80% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com